上式をその上の波動方程式に代入すると、下式に示す3次元ヘルムホルツ方程式が出来上がります。
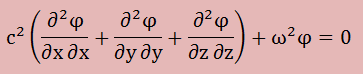
ここに、c2=P/ρ。大気圧下では、P=101325Pa, ρ=1.225Kg/m3ですので、c=約340m/sになります。 これまでに長々と式の導出をしてきました。ここでもう一度確認ですが、解析から何を求めようとしていたかと言うと、固有値でした。結局、独立変数が架空のポテンシャルであろうが圧力変動であろうが、式からえらるのものは、複数の固有値とその固有ベクトルです。ようするに、式の最終形が波動方程式であれば固有値は計算され、固有振動数は、音速とその固有値で決まるのです。 ここでは、そのヘルムホルツ方程式として、技術分野でなじみの深い下の式で音響振動の固有値問題の求め方を紹介します。上の式の展開で示した通り、下式は正しい表現ではありませんが、必要な固有値とその固有ベクトルは得られます。
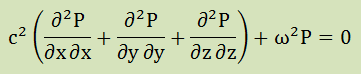
ここに、Pは圧力変動、α2=ω2/c2、ω=圧力波の周波数(rad/s)、c=流体内の波の伝播速度(空気の場合はc=340m/s)です。境界条件としては、自由振動(natural oscillation)を考慮するため、圧力波の完全反射を全ての境界に与えます。つまり、自然境界条件の∂P/∂n=0になります。
■音響解析の有限要素法■
有限要素法で固有値問題を解くには、これまでと同様に下の積分式から始める必要があります。
考え方は、1次元のHelmholz Equationとまったく同じです。
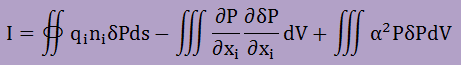
上の式の境界積分項にあるqiは、境界での∂P/∂xiを意味しています。更に、要素を使って未知数Pを近似し上の式に代入すると、下式が得られます。
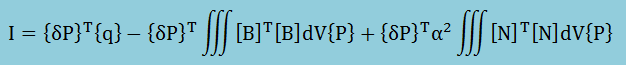
重み付け残差法のルールに従い、積分値(I)を{δP}で微分しゼロ(∂I/∂{δP}T=0)とおくと、下の式に示す様に要素の有限要素式が得られます。
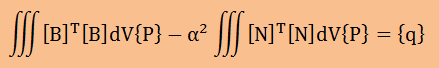
| BACK | NEXT |
|---|
| Menu | LU Decompo | Stiff | 3D Solid | 3D Fluid | Eigen&Lanczos | Sound Eigen | Solid Eigen | Solid Axisym |