まず、領域内での媒体(空気)の質量保存の法則を書いてみましょう。下がその3次元のしきです。
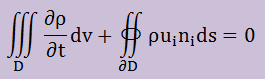
ここに、ui=媒体のi軸方向の速度を表しています。 上式の境界積分の項に発散の定理を施すと下が得られます。
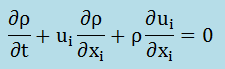
ここで仮定ですが、媒体の密度(ρ)は圧力(P)のみの関数としています。つまり、P/ρ=nRTです。 また、∂ρ/∂xiは微小ということで無視することにします。 更に、P/ρ=c2と近似しています。すると、ρ=P/nRTを上式に代入し、全体にnRTを掛けると上式は、次のようになります。
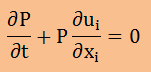
上の式をみると、独立変数にPとuが有ります。ということで、次にPとuを関連付ける架空のポテンシャル(Ψ)が必要になってきます。文献によると、以下を定義しています。
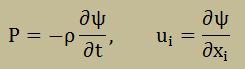
これらを質量保存の式に代入し、全体をρで割ると、以下になります。
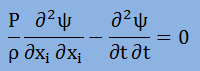
ということで、3次元の波動方程式が導きだされました。膜や弦の場合の波動方程式では、P=τ=膜や弦内の張力、ρ=膜や弦内の密度、Ψ=膜や弦内の平衡状態からの変位、となっています。
そして、共振現象(resonance)や調和振動の応答(harmonic response)を調べる場合は、波動方程式のポテンシャルΨ(x,y,z,t)を次の式で書き表すことができます。
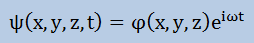
ここに、ω=波の周波数(Wave frequency)、i2=-1です。
| BACK | NEXT |
|---|
| Menu | LU Decompo | Stiff | 3D Solid | 3D Fluid | Eigen&Lanczos | Sound Eigen | Solid Eigen | Solid Axisym |