上式を全ての要素に対して計算を行い、グローバルマトリックスに足し込むと、以下の連立一次方程式が出来上がります。
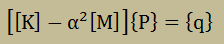
ここに、[K]は∫∫∫[B]T[B]dVを、そして[M]は∫∫∫[N]T[N]dVをグローバルマトリックスに足し込んだ結果です。 次に行うことは、領域を完全な閉空間にします。つまり、自由振動を得るために境界で圧力波が完全に反射する様にします。そのためには、Neumann境界条件を与え、{q}={0}にしなければなりません。すると、連立方程式は、下式の様になります。
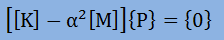
上式の圧力分布を表す{P}は、α2がゼロの場合、{P}={0}または{P}={一定値}になります。この解のことを特に意味の無い解(Trivial solution)と言って固有値ではありません。しかし、圧力波は、自由振動するわけですから、{P}≠{0}になっているはずです。したがって、上式の連立方程式を満足させるためには、下の式が必要条件になります。
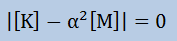
つまり、マトリックスの行列式がゼロになるα2を探す問題になります。これを固有値問題(Eigenvalue Problem)と言い、固有値α2は、実数で正の値になることが知れています。そして、ω2=c2α2のωを固有周波数(Characteristic frequency) といいます。また、その周波数に対応する{P}を固有ベクトル(Eigenvector)と言い、その周波数による振動をモード(Mode)と言います。行列式がゼロになるα2はたくさん存在しますので、固有周波数とモードもたくさん存在することになります。全座標軸方法に振動する一番低い周波数のモードを基本固有モード(Fundamental mode)といいます。領域が矩形(Lx×Ly×Lz)の場合、固有値の厳密解は以下の式で得られます。式のl=m=n=1の場合が基本固有モードと呼ばれています。
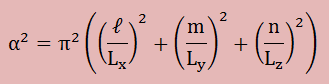
■固有値の計算方法■
固有値の計算方法は、例題を交えて
Eigen&Lanczos
で紹介しましたが、もう一度、有限要素法で得られた連立方程式をスタート点として
固有値が計算されるまでを復習してみます。
有限要素法でHelmholtz 型微分方程式を離散化し自由振動の境界条件を与えると以下に示すマトリクス型の 連立方程式を導かれます。ここでは、固有ベクトル{P}の代わりに{x}を使います。
| [K]{u}=α2[M]{u} |
| BACK | NEXT |
|---|
| Menu | LU Decompo | Stiff | 3D Solid | 3D Fluid | Eigen&Lanczos | Sound Eigen | Solid Eigen | Solid Axisym |