下は、固有振動周波数をスペクトル風にプロットしてみました。横軸は周波数(Hz)で縦軸はNORMの対数です。数値が大きいほど固有値と固有ベクトルの計算精度が高いことを示しています。
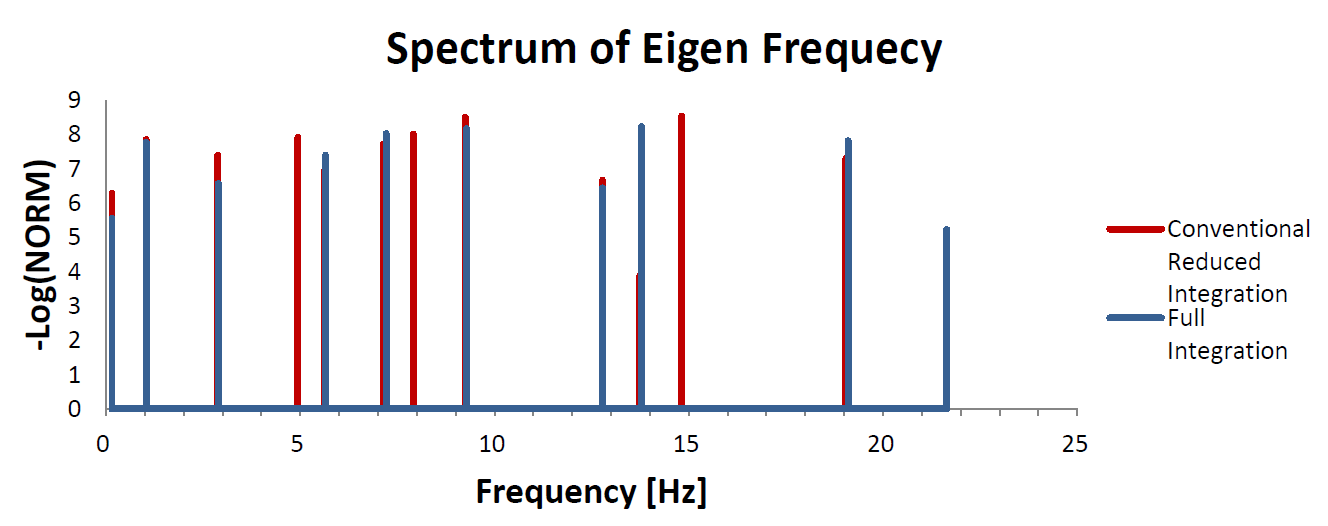
赤色が従来型の低減精度積分によるものです。図に示されている通りに、ビームに存在しない振動モード(4.9377721Hz, 7.918034Hz, 14.812998Hz)が現れているのが解ります。低減精度積分の要素を使うときには、この辺の短所を十分理解した上で解析を行う必要があります。
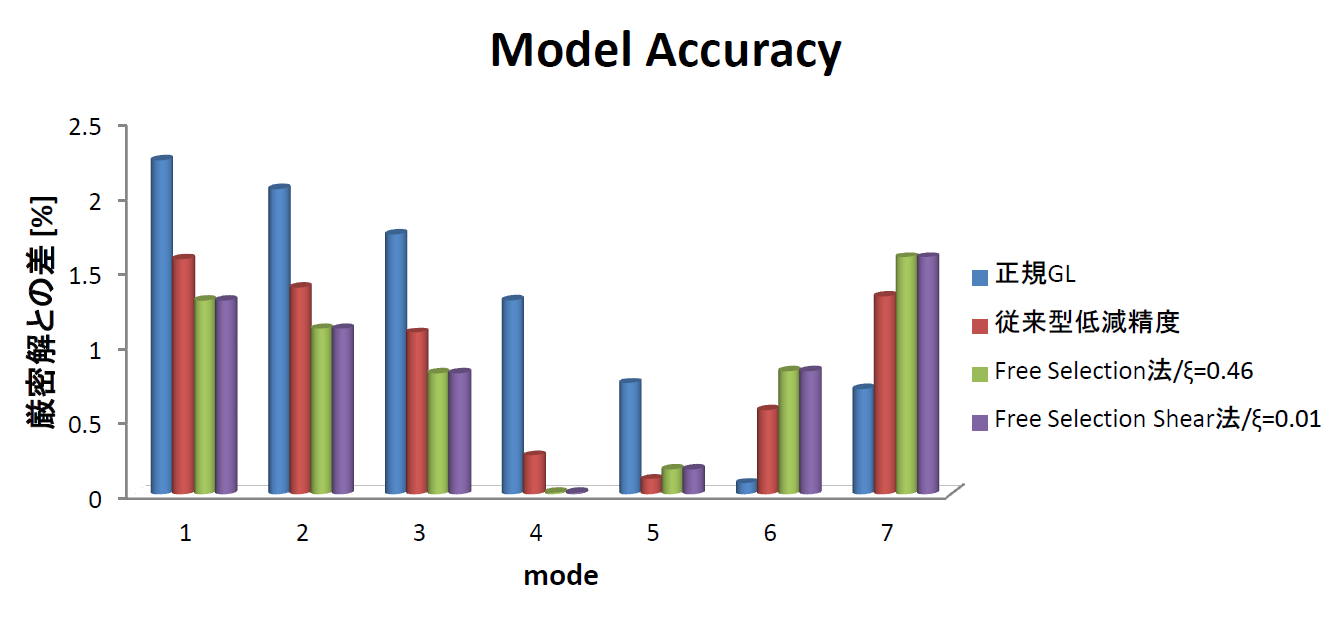
要素単位の積分の精度を高めようとすると、どうしてもGauss-Legendre法を使ってしまいます。しかしこれは要素のみに有効で、要素間のことはまったく無視した積分の方法と言えます。要素間をいかに表すかが有限要素法の特徴です。要素タイプによっては、要素間を十分考慮にいれた積分を行う必要があります。1次要素では、要素のアスペクト比に従いFree Selection法で積分を行うことで計算精度を2次要素と同じレベルに上げることが可能です。Free Selection法の良い点は、計算精度をコントロールでき、かつ“やじろべえ”効果による振動を発生させないということです。
| BACK | NEXT |
|---|
| Menu | LU Decompo | Stiff | 3D Solid | 3D Fluid | Eigen&Lanczos | Sound Eigen | Solid Eigen | Solid Axisym |