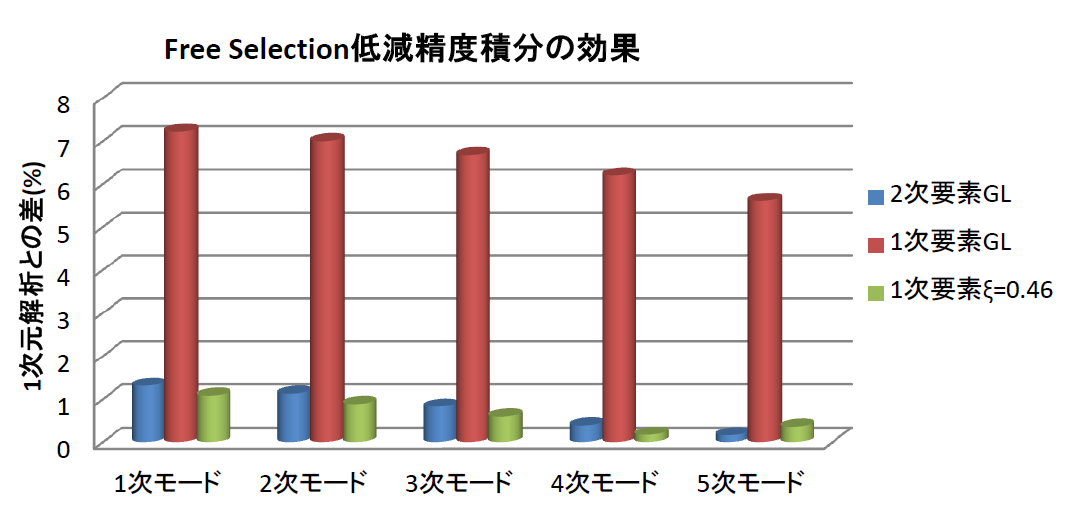
1次元解析の値をベースとして上の表をグラフにすると以下のようになります。グラフの縦軸は1次元解析との差を%で表してあります。図を見ると他の振動モードでもξ=0.46のFree Selection低減精度積分は2次要素よりの良い結果を出しています。
下図は積分点の値(ξ)を横軸に、1次固有振動数を縦軸にとった時のグラフです。グラフ内の●の点はGauss-Legedre法、●は台形則を意味します。前にも言いましたが、Free Selection低減精度積分の長所はアワーグラスの振動がまったく出ないということです。
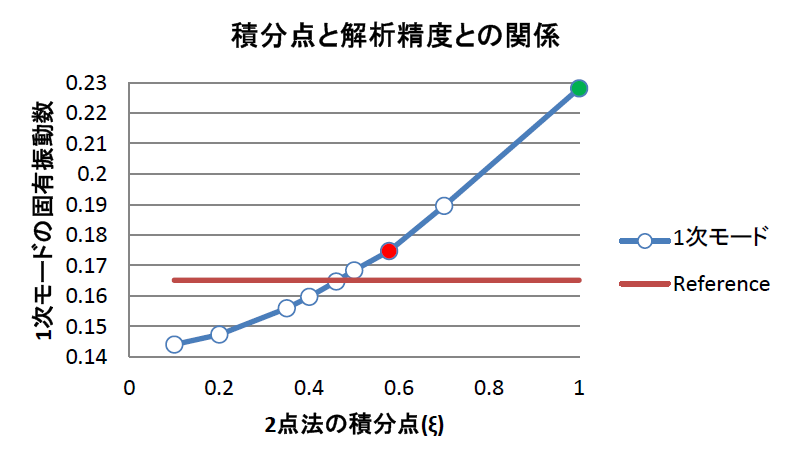
積分点が要素の節点に近づく程、1次固有振動数の値は大きくなり、要素の中央に近づく程小さくなります。つまり、積分点が要素の中央にあるときが一番柔らかく、節点にあるときが一番硬くなっています。Referenceは、1次元解析の厳密解です。
結局、要素毎の積分であれば確かにGauss-Legendre法は精度良く積分してくれますが、要素のAssembleを考えると計算結果として少し硬い目のビームになっているということです。台形則だともっと硬くなります。つまり、積分方法が間違っているのでなく、せん断応力の項の取り扱いに問題が有るということです。今のところ良いせん断応力の項の処理方法が無いので積分法でごまかしているということでしょう。境界要素法だとこのような問題は起きないようですので、なんとか剛性マトリクスの積分を境界要素法とのHybridが出来ると良いですね。しかし、境界要素法はコーナー問題が有るのでちょっと難しいかも。
| BACK | NEXT |
|---|
| Menu | LU Decompo | Stiff | 3D Solid | 3D Fluid | Eigen&Lanczos | Sound Eigen | Solid Eigen | Solid Axisym |