要素:8節点1次ヘキサ
要素のアスペクト比: 1
Beamの境界条件:片持ち梁
検証モード:1次の固有振動数
要素分割:100X2X2, 150X3X3, 200X4X4, 250X5X5, 300X6X6, 400X8X8, 500X10X10
無次元座標ξの値:0.577350269189626, 0.5, 0.46, 0.4, 0.35

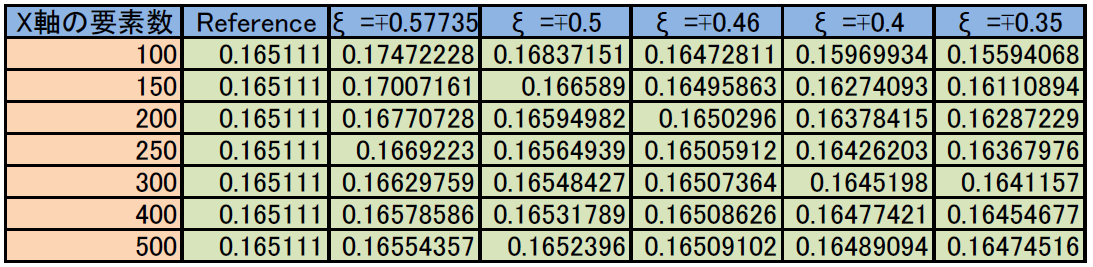
表中のReferenceとは、計算領域を2次要素でx軸方向を200要素で分割したときの計算結果です。Referenceがここでは正解ということにしておきます。

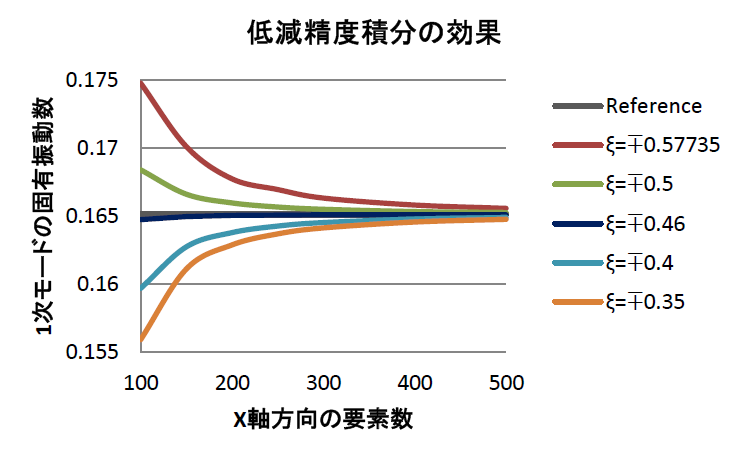
計算結果をみると、ξ=+/-0.46ではどんな要素分割でもReferenceとほぼ同じ値を出し安定した解を提供してくれています。低減精度積分は、ここで紹介したように良い結果をもたらしてくれますが、信頼度の面ではいま一です。したがって、固有値解析でも2次要素が精度が良く安定した要素ということになります。

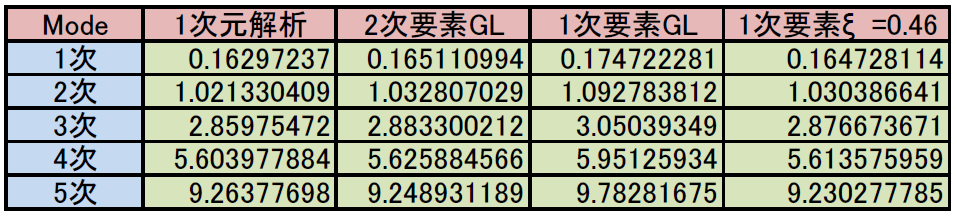
確認のために他のモードの精度もチェックしてみました。要素分割は100X2X2です。積分点をξ=+/-0.46で計算すると、 このような結果が出力されます。1次元解析、2次要素解析、Gauss-Legedre積分による1次要素解析とともに計算結果を以下に示します。表のGLとは通常のGauss-Legedre積分を意味します。