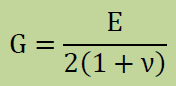
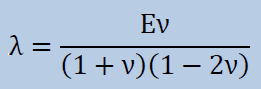
以前の式に無かったのが、φiがある表面積分です。この項は、弾性体の動きを摩擦で抑制します。 一般に摩擦力(f)はf=-C∂u/∂tで表されます。この項は法線の力をτjinjから取り除くために、 ちょっと複雑な表現になっています。
次にuiを下に示すように時間と空間に変数分離します。
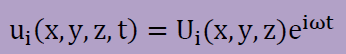
そして、上の式をNavierの方程式に代入すると、以下の新しいNavierの方程式が得られます。 式中のiωのiは、複素数のiです。摩擦力は位相が90度ずれることになります。下の式を解くことを複素固有値解析 と呼ばれ、ブレーキ等の固有値計算に用いられています。
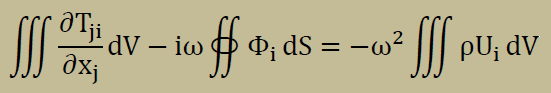
式中の各項に現れるシンボルの詳細は以下のようになっています。
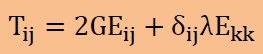
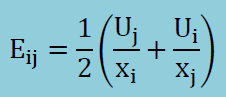
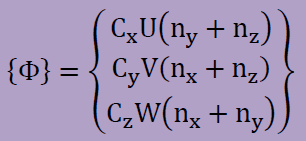
そして上のNavierの方程式に重み付け残差法の手順を施すと、1つの要素に対し最終的に以下の有限要素式が得られます。
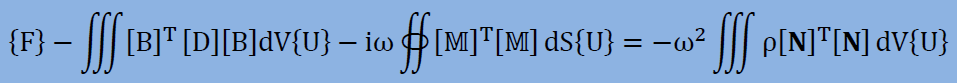
| BACK | NEXT |
|---|
| Menu | LU Decompo | Stiff | 3D Solid | 3D Fluid | Eigen&Lanczos | Sound Eigen | Solid Eigen | Solid Axisym |