すると下表の片持ち梁の固有振動周波数が得られます。
| Mode | λ | f(Hz) |
|---|---|---|
| 1 | 1.87510406871196 | 0.164996949 |
| 2 | 4.69409113297417 | 1.03401823 |
| 3 | 7.85475743823761 | 2.895280986 |
| 4 | 10.9955407348754 | 5.673595186 |
参考までに、両端が自由支持だった場合の固有振動周波数は以下のようになります。
| Mode | λ | f(Hz) |
|---|---|---|
| 1 | 4.73004074486270 | 1.049916898 |
| 2 | 7.85320462409583 | 2.894136357 |
| 3 | 10.9956078380016 | 5.673664435 |
| 4 | 14.1371654912574 | 9.37885552 |
3次元の固有振動解析を実施した場合、少なくとも上の表に示した周波数は出てくるはずです。しかし、1次元ではPoisson比が 展開式に最初から有りません。ですから、3次元の固有振動解析を行い結果を1次元と比較する場合、Poisson効果がなるべく 出ないように境界条件を設定しなければなりません。
■3次元弾性体の運動方程式と固有値■
弾性体構造物の運動を再現してくれるのが、Navierの方程式です。以前Solidでも紹介したことがあります。
今回は振動の抑制項を入れた状態から話を進めたいと思います。下の式を見て下さい。
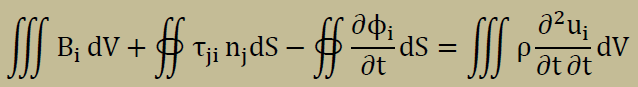
式中の各項に現れるシンボルの詳細は以下のようになっています。
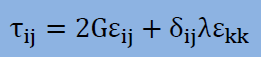
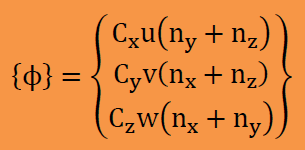
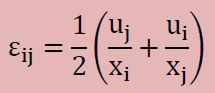
| BACK | NEXT |
|---|
| Menu | LU Decompo | Stiff | 3D Solid | 3D Fluid | Eigen&Lanczos | Sound Eigen | Solid Eigen | Solid Axisym |