次に[A]{u}₁を計算し{y}と置きます。[A]として前に使った行列を用いることにしましょう。

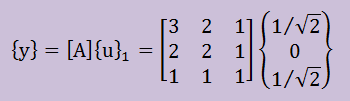
[A]{u}₁を計算しているということは、Krylov列の性質がこのLanczos法にも盛り込まれていることになります。 次に{y}^T{u}₁を計算しα₁と置きます。ここで、式に一般性をもたすために、 添え字の数字の代わりに文字jを使うことにします。つまり、以下になります。

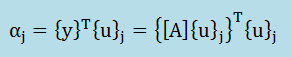
正規直交ベクトルの非直交成分を取り除くために以下を計算します。ここで注意ですが、 添え字jが1のときβ₀と{u}₀を参照しています。

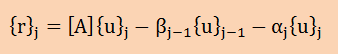
ここに、β_jはベクトル{r}_jの長さを示します。つまり以下で計算できます。 また、{u}₀はゼロベクトルですので、β₀はゼロになります。

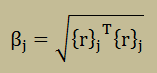
すると、次の正規直交ベクトル{u}_j+1は以下になります。

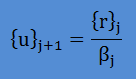
上の計算をα_n, β_n−1, {u}_nが得られるまで繰り返し、 下に示す行列[T]の所定の位置に埋め込みます。 ここに、nは行列[A]のサイズです。すると行列[A]は三角対角行列[T]に変換されたことになります。 固有値は維持されています。つまり、[A]の固有値=[T]の固有値ということです。

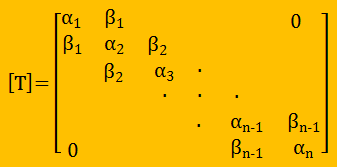
Page 17中