例題で使ったマトリクスを使って実際に[T]を生成し固有値を計算してみましょう。 まず、[T]ですが上の式に従って計算すると、以下が得られます。

上の[T]をPower法で固有値を計算すると、以下が得られます。

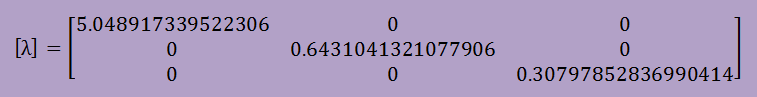
計算結果は、以前と同じが得られました。しかし、行列[A]を三角対角行列[T]に変換し、 Power法で計算しても計算量の削減にはつながりません。せっかく三角対角行列にしたのに、 計算の過程でフルマトリクスになってしまいます。
三角対角行列をうまく活用する方法にdet[[A]-λ[I]]=0をベースとしたBisection法があります。 以下にその方法を紹介しておきましょう。その前に、１つ確認しておきたいことがあります。 それは、Lanczos法の冒頭で述べたように[U]^T[A][U]=[T]の関係式がありました。 [U]はLanczos法で得られた正規直交ベクトルです。固有ベクトルではありません。

■[T]が三角対角行列になる理由■
その前に、[T]はどうして、三角対角行列になるのでしょうか。 本当にそうなるのかを、3×3の行列[A]で確認しておきましょう。まず、使う記号を簡略化するため、以下のように定義します。 今後の取り扱いの便宜上正規直交ベクトル{u}₁, {u}₂, {u}₃を{u}, {v}, {w}で 置き換えてあります。

ここに、式中の定数は、以下のようになっています。

絶対値記号は、ベクトルの長さを意味します。