そして[U']=[P][U]を計算すると、以下が得られます。
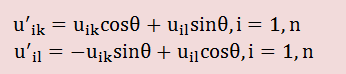
上の計算が終了したら、また非対角要素で絶対値が一番大きいaklを取り上げて、 上と同じ計算を行います。このプロセスを繰り返すと、しまいには[A]の非対角要素の全ては ゼロになり、対角要素は固有値になります。
回転角度θですが、実際のプログラムではcosθとsinθを計算するためにarctan関数を使う ことはありません。以下のステップでcosθとsinθを決定します。
| akk-all=0の場合は、cosθ=1/√(2), sinθ=1/√(2)とします。 ただし、 akl<0であればsinθ=-1になります。 そして、akl=0の場合は、cosθ=1, sinθ=0 |
| それ以外の場合は、以下の方法でcosθとsinθを計算します。 |
| r=(1/2)√((akk-all)2+(2akl)2) |
| cos2θ=|akk-all|/(2r) |
| sin2θ=akl/r |
| cosθ=√((cos2θ+1)/2) ただし、akl<0であればcosθ=-√((cos2θ+1)/2) |
| sinθ=sin2θ/(2|cosθ|) |
ここで説明したJacobi法については、JACOB35.FORを参考にして下さい。 プログラムを実行すると、計算結果はファイルJACOB.OUTに入ります。Power法と同じ例題を計算していますので、 計算結果を検証してみて下さい。
■厳密法/三角対角行列に変換■
フルマトリクスだと計算が大変だということで考え出されたのが、フルマトリクスを一旦三角対角行列に
変換した後、固有値を計算するという考えが出てきました。三角対角行列を用いた固有値計算の代表的な
方法にdet[[A]-λ[I]]=0をベースにしたBisection法があります。三角対角行列とは、行列の対角要素と
その両隣の対角のみに数値が入り他はゼロになっている行列のことです。
■Lanczos法による三角対角行列生成■
三角対角行列を作る方法の1つです。Lanczos法は、Krylov列から順次、[A]の正規直交規定系
[U]=[{u}1, {u}2,…,{u}n]を生成し、そして[A]と[U]から
[T]= [U]T[A] [U]の三角対角行列を生成します。
条件としては、[A]が対称でなければなりません。Lanczos法の計算手順を以下に紹介します。
最初に{u}1を作る必要があります。このベクトルの長さは1です。例えば、以下が考えられます。
[A]の対角要素を使って{u}1を作っても問題ありません。この場合でも、ベクトルの長さは1で
なければなりません。
また、計算上{u}0も定義しておく必要があります。
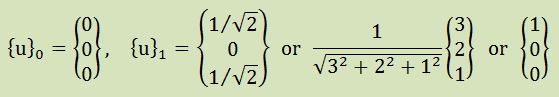
| BACK | NEXT |
|---|
| Menu | LU Decompo | Stiff | 3D Solid | 3D Fluid | Eigen&Lanczos | Sound Eigen | Solid Eigen | Solid Axisym |