すると、行列[A]と[U]の積は[A]{x}i=λ{x}iの関係から[A][U]=[U][λ] が言えることは前にも言いました。 上式の両辺に前から[U]-1を掛け算してみます。すると、以下の結果が得られます。 これも前に言いました。
| [U]-1[A][U]=[λ] |
上式で行列[A]を変換することを、代数学では相似変換(similar transformation)といいます。 または、[A]と[λ]を直交相似(orthogonally similar)と言います。 そして、相似変換しても[A]と[λ]の固有値は変化しません。
上の式の[U]と[λ]ですが、どうすれば得られるかがここでの問題です。 そこで、[U]は簡単にえられませんが、ある一つの直交行列なら簡単に作れます。 これをいま[P]1としておきましょう。そして[A]=[A]1とします。すると、以下の結果がえられます。
| [P]-11[A][P]1=[A]2 |
ここで重要なのが[A]1と[A]2の固有値には変化はありません。更に以下を計算します。
| [P]-12[A][P]2=[A]3 |
この計算をうまく行うと、終いには上式の右辺が対角要素の行列になります。つまり、以下のよう右辺が固有値になります。
| [P]-1n[A][P]n=[λ] |
そして固有ベクトルの入った直交行列[U]は以下で計算されます。
| [U]=[P]1[P]2............[P]n |
では、どのような[P]でどのような計算手順なら固有値行列[λ]が得られるのでしょうか。 ということで、まず、 下のように[A]が2×2の行列だった場合を考えて見ましょう。
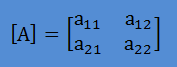
この場合、a12およびa21がゼロになる[P]があれば、[λ]を簡単に手に入れることができます。 前にも言いましたが、この問題は、弾性力学で2次元の主応力を計算するのと全く同じ問題です。 [A]の対角要素が、τxxとτyyの法線応力に、非対角がτxyのせん断力に値します。 つまり、{x}1を x1= cosθ i- sinθ j とすると(長さは1)、直交する{x}2は以下のよう書けます。
| BACK | NEXT |
|---|
| Menu | LU Decompo | Stiff | 3D Solid | 3D Fluid | Eigen&Lanczos | Sound Eigen | Solid Eigen | Solid Axisym |