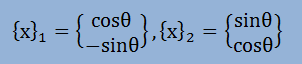
よって、[P]は以下のようになります。
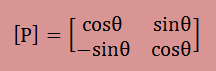
また、[P]の逆行列は以下になり、このような場合、[P]-1= [P]Tになります。
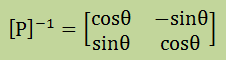
[P]がわかれば次は、a21がゼロになるθを計算することにより 固有値a'11とa'22を得ることができます。つまり、 下の式[P]-1[A][P]=[A']を満足するθを計算します。
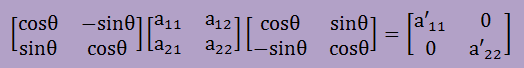
角度θはa'12=0より以下で計算できます。主応力のときと同じ式になります。
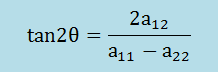
角度θが分かれば固有値a'11とa'22は、上の行列演算より以下のようになります。
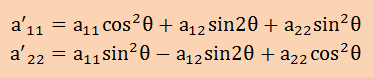
そして固有ベクトルは、以下で計算できます。
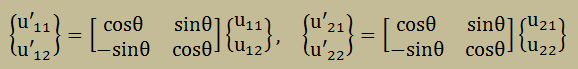
ここに、初期固有ベクトルとして最も簡単で確実なものとして以下が考えられます。
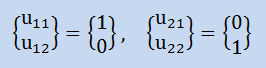
| BACK | NEXT |
|---|
| Menu | LU Decompo | Stiff | 3D Solid | 3D Fluid | Eigen&Lanczos | Sound Eigen | Solid Eigen | Solid Axisym |