つまり、厳密法がn×nのフルマトリクス[A]の固有値を計算するのに対し、近似法はn×nの[A]を一旦m×mの[T]に縮小した後に
固有値を計算する方法を言います。
Power法の計算プログラムについては、POWERMETHOD2.FORを参考にして下さい。
Power法を離れる前に確認しておきたいことがあります。前に固有値およびそれらの固有ベクトルは、[A]に対し
[U]T[A][U]=[λ]の関係にあると言うことを伝えました。この関係式をもうちょっと深く掘り下げてみましょう。
まず、3×3の行列を使うと[U]T[A][U]=[λ]は、次のように書けます。
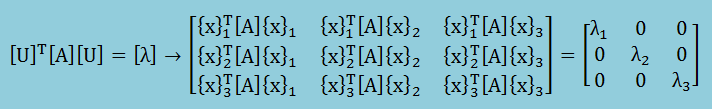
[A]{x}i=λi{x}iでしたから、上の式から{x}iT{x}j=0
ということになります。ここにi≠j。つまり、{x}iと{x}jは直交していることになります。
ここで紹介したPower法を使う上での注意点があります。この方法は計算の過程でベクトルの長さを計算します。この長さが固有値になりますから、負の固有値はあり得ないということになります。殆どの技術問題に主応力計算を除き負の固有値はありえません。どうしても負の固有値も計算したい場合は、マトリクス[A}の対角要素にバイアス(ある大きな値:Bisection法の所で説明)を加算しておく必要があります。
■Jacobi法■
最も良く知られた方法にJacobi法があります。これは、対称行列に適用され、固有値と固有ベクトルを
同時に求める繰り返し計算手法です。相似変換(ギブンス回転)を実行すると行列の非対角要素がゼロになります。
応力の計算で出てくる主応力の計算方法と似ていて、せん断応力をゼロにさせる座標回転が
ギブンス回転と同じ操作になります。
この計算を進めると対角要素のみに数値が残り、その中には固有値がはいることになります。
非対角要素をゼロにするためには、繰り返し演算が必要になります。
Jacobi法の原理ですが、まず、固有値の定義からスタートしましょう。行列[A]の固有値λiと
固有ベクトル{x}iは以下の代数式を満足していなければなりません。
| [A]{x}i=λ{x}i |
前にも言いましたが、固有ベクトル{x}iは、自身を除き全ての{x}jに対し直交していなければなりません。 つまり、{x}iT{x}jに=0 (i≠j)です。また、固有ベクトル{x}iの長さは1です。 そして一般性を考慮し行列[U]と[λ]を以下のように定義しておましょう。 つまり、[U]は全ての固有ベクトルを一つにまとめて行列です。 [λ]は対角要素に固有値が入りその他の要素にはゼロが入ります。
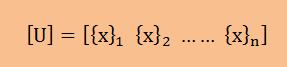
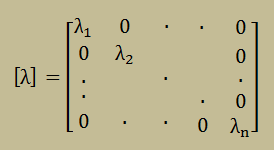
| BACK | NEXT |
|---|
| Menu | LU Decompo | Stiff | 3D Solid | 3D Fluid | Eigen&Lanczos | Sound Eigen | Solid Eigen | Solid Axisym |