上で言いましたが、[A]{x}=λ{x}から得られた計算結果を総合すると[A][U]=[U][λ]となります。 この式の両辺の後ろから[U]^Tを掛算してみます。すると以下のように書けます。

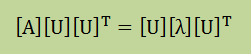
まず、[U][U]^Tですが、これは言うまでもなく[I]になります。次に[U][λ][U]^Tを調べてみましょう。 検証がちょっと煩雑になりますが、以下の結果を得ることができます。

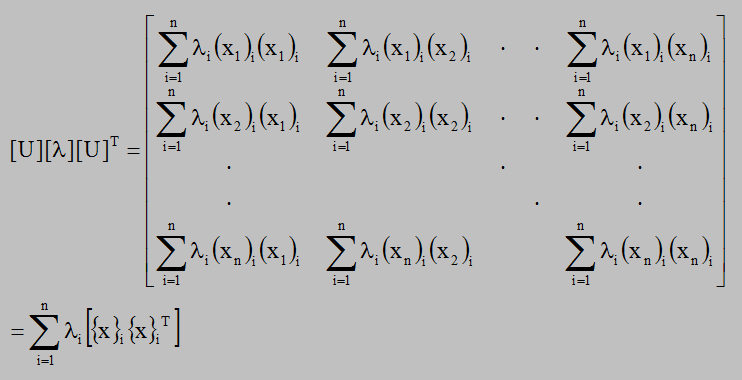
結果的に[A][U][U]^T=[U][λ][U]^Tは以下になります。

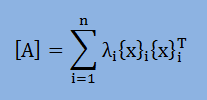
[A]が固有値と固有ベクトルとで合成されていることがわかりますね。

例題の3×3の行列に話を戻しますと、オリジナルの[A]から最大固有値が計算されました。 つまり、上式の右辺にある最大固有値λ₁とベクトル{x}₁が[A]から抽出されたことになります。 ですから、次に大きい固有値を計算するためには、以下の操作を[A]に対して行わなければならにことが解ります。

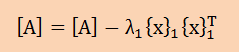
すると残された[A]には2番目に大きい固有値と最小の固有値が入っています。ですから、[A]にべき乗法を施すと、 2番目に大きい固有値を出してくれることになります。 これで一応、固有値と固有ベクトルの計算はできたことになります。しかし、計算量を考慮に入れると、 べき乗法は実用的ではありません。マトリクスのサイズが大きくなると計算時間は更に増し、また収束は遅いと思われます。
固有値を計算する方法には、べき乗法の他に様々な方法が考案されています。 書物等では直接法と反復法のような分類がありますが、固有値が5個以上の場合、全てが反復法になってしまいます。 よって、ここでは厳密法と近似法に分類してそれらの方法の幾つかを紹介します。 ここでの厳密法とは、全ての固有値が計算できることを指します。べき乗法はこの中に入ります。 それに比べ近似法は、フルマトリクス[A](n×n)の固有値問題を[A]より数段小さい部分空間マトリクス[T](m×m)に射影してから固有値を計算する方法を意味します。この部分空間に射影された固有値問題は、厳密法で解くことになります。