また、固有値の特徴から固有ベクトルの直交性というのがあります。 つまり、計算された固有ベクトルは以下を満足していなければなりません。
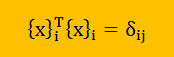
ここで少し理屈の話をしておきます。代数学の書物を読むと、固有ベクトルを1つにまとめて行列[U]としています。 式で書くと以下になります。
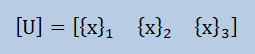
上で計算した固有ベクトルを使うと[U]は以下になります。

注意:対称行列[A]がn×nの場合は、[U]もn×nの対称行列になります。
これまでに紹介してきたべき乗法の計算結果を1つの式で表してみます。 固有値の定義([A]{x}=λ{x})から計算結果を総合すると[A][U]=[U][λ]と書けます。 両辺に前から[U]−1を掛算すると以下になります。
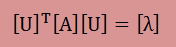
ここに、[U]が直交固有ベクトルで出来ている場合、[U]T=[U]-1になります。 また、マトリクス[λ]は以下のように書きます。
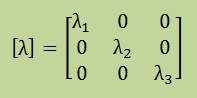
計算例の場合、[λ]は以下になります。
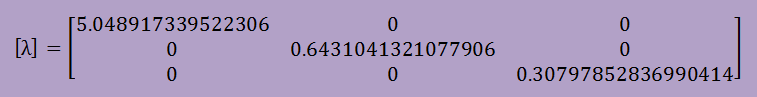
| BACK | NEXT |
|---|
| Menu | LU Decompo | Stiff | 3D Solid | 3D Fluid | Eigen&Lanczos | Sound Eigen | Solid Eigen | Solid Axisym |