固有ベクトルの計算については、別のコーナーで詳しく説明します。
以上のことから、 [A]がn×nのマトリクスの場合、行列式はλのn次代数式になります。つまり、 固有値を導き出すということは、n次代数式の根を探すのと同じことなのです。 または、その代数式を因数分解することとも同じことなのです。これは大変な作業になります。 これをなんとかしようと考え出されたのが数値計算法です。以下にそれらを紹介します。 手始めに最も簡単なPower法から紹介します。

■Power Method (べき乗法)■
大昔の数値計算法の本を開くと必ずと言ってよいほど見かける固有値の計算手法がここで紹介する方法です。 この方法は、Krylov列の性質を利用した計算方法と書いてあります。それは一体何か？。 大きさがn×nのマトリクス[A]とベクトル{u}₁によって生成されるm個の ベクトル列[{u}₁, [A]{u}₁, [A]² {u}₁,…, [A]^m-1 {u}₁]をKrylov列と呼ばれていて、mが無限大のときKrylov列は [A]の最大固有値に対応する固有ベクトルに収束するという性質を持っています。 何のことか解り難いのでまずは、計算してみましょう。[A]は上で紹介したものを使います。 そして、最初のベクトル{x}として下を用います。このベクトル長さは１です。

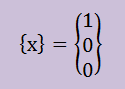
そして、[A]{x}={y}の{y}を計算します。結果は、以下のようになります。

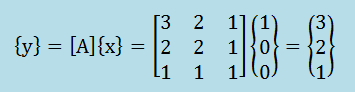
ベクトル{y}の長さ、つまり近似固有値(λ)を計算すると、3.7416573867739413になります。 そして{x}={y}/λを計算し新しい固有ベクトル{x}とします。結果は以下のようになります。

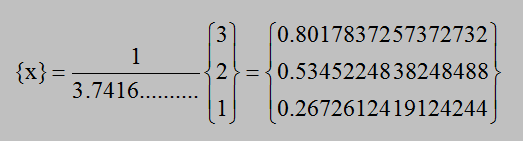
そしてまた[A]{x}={y}の{y}を計算し近似固有値(λ)と新しい固有ベクトル{x}を計算します。 これを繰り返すと絶対最大固有値とその固有ベクトルに収束します。 以下に9回計算を繰り返した結果を示していますが、実際は固有ベクトルの全ての要素が収束するまで行います。