例えば、以下の3×3の対称行列(Symmetric matrix)の場合を考えてみましょう。

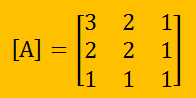
を計算すると、次のようになります。固有値λの3次式になっていますよね。 つまり、以下の式を因数分解できれば固有値を得たことになります。

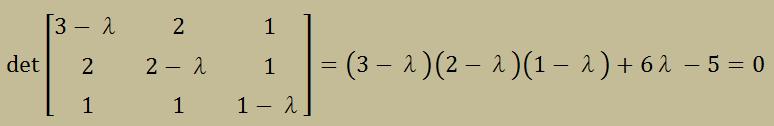
マトリクス[A]が3×3ですから、 はλの3乗の代数式になり、図にすると以下のようになります。 下図の曲線が横軸と交わる点が固有値になります。つまり、行列式がゼロになる点です。

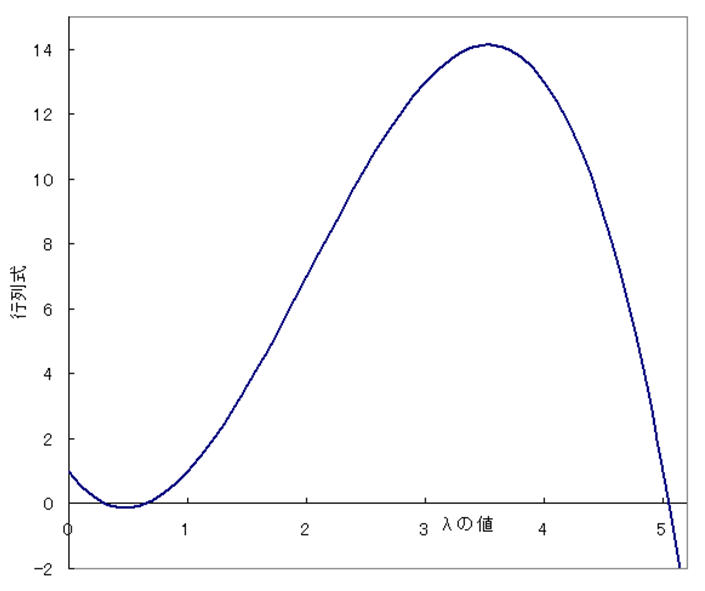
表計算ソフトを用いて精密に計算すると固有値はλ₁=0.3079785, λ₂=0.6431042, λ₃=5.048917になります。つまり、以下のように因数分解されたことになります。