■Newton-Raphson法による主応力の計算■
この方法は主応力のみを計算してくれますので、座標軸のベクトルはInverse Power法などで計算する必要があります。この方法は下のマトリクスの行列式のInvariantsを使って逐次計算を組み立て、エネルギーで収束をチェックします。
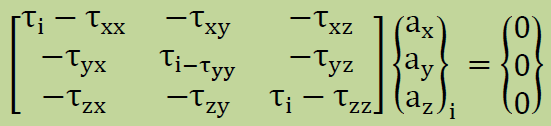
上のマトリクスの行列式を計算すると、次の3次式が得られます。この3次方程式の根は全て実根であることが証明されています。Cardano法での3次方程式をそのまま使ってのよかったのですが、ここでは出来るだけ材料力学の形に従うことにしました。
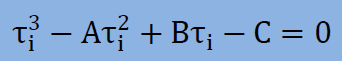
ここに、上式のA, B, Cは以下のようになっています。
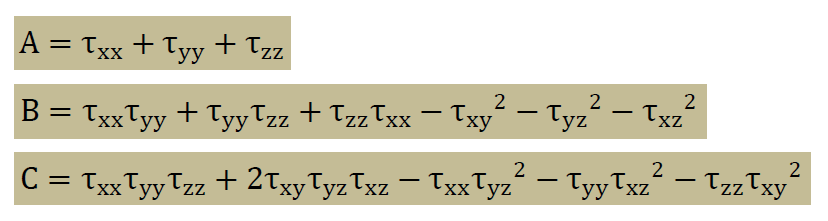
物体に力を掛けて得られる各点の主応力は、計算で用いた座標軸に無関係に決まる値です。ですから、上のA, B, Cはその座標軸をどのように回転しても値は変わることはありません。ですから上のA, B, C のことをInvariantsと呼びます。 更に、全てのせん断応力がゼロになっている状態でもA, B, C の値は変化しません。ですから、以下が言えます。
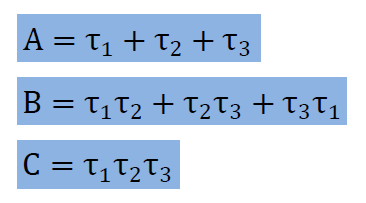
上の式をここでは条件式と呼ぶことにします。また、エネルギーの概念から以下の式EとE’もInvariantsに数えることができます。
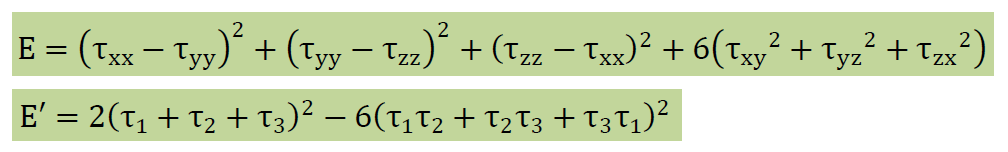
| BACK | NEXT |
|---|
| Menu | LU Decompo | Stiff | 3D Solid | 3D Fluid | Eigen&Lanczos | Sound Eigen | Solid Eigen | Solid Axisym |