そしてここでは以下の両エネルギーの式の差をδEで定義しておきます。
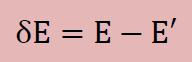
Eは解析で便宜上予め設定したxyz座標での応力τijによるエネルギーで、E’は主応力の座標上でのエネルギーを示します。したがってδEはゼロになければなりません。しかし、E’が主応力近傍によるエネルギーだとゼロでないδEが発生することになります。このδEをゼロに近づける方法が有れば主応力を得ることができます。
では、どのようにすれば全ての主応力が計算できるかです。3次式を解くのも一手ですが、全ての主応力が実根という事実を利用すると、繰り返し計算で全ての主応力を得ることができます。以下は主応力を得る1つの手法として理解しておいて下さい。 まず、条件式を以下に示すようにゼロ関数(fi)として定義します。全ての主応力が計算されたとき、以下のゼロ関数(fi)は全てゼロになります。ここに、式の≡は定義するという意味です。式中のA,B,Cはxyz座標上で計算されたInvariantsです。
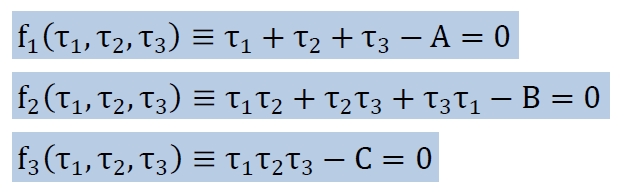
しかし、繰り返し計算ですから、計算の開始時点で推測の主応力が必要になります。もちろんこの場合ゼロ関数はゼロになっていません。そこで、f1, f2, f3をテーラー展開しNewton-Raphson法で推測の主応力をより真に近づけます。以下になります。
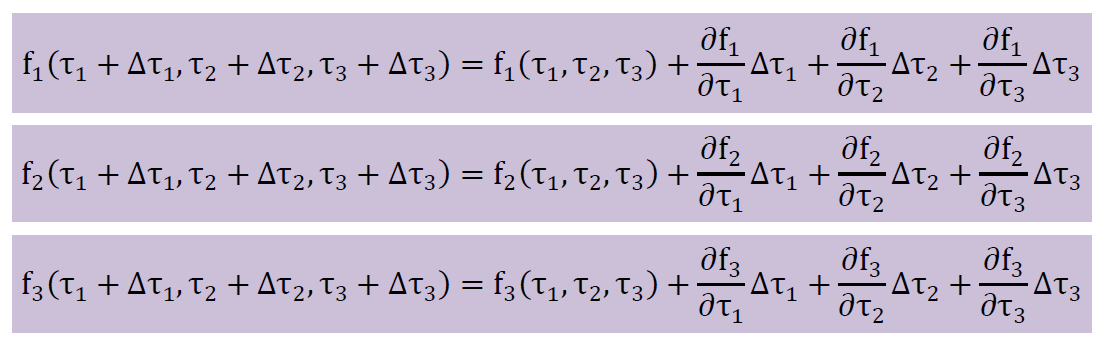
上式の左辺がゼロになっていると仮定すると、Δτ1, Δτ2,Δτ3は以下で計算できます。ここでは、下のマトリクスを[D]と呼ぶことにします。
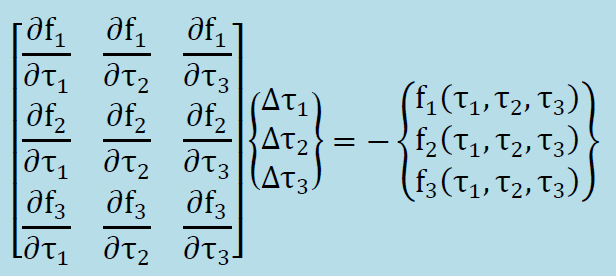
| BACK | NEXT |
|---|
| Menu | LU Decompo | Stiff | 3D Solid | 3D Fluid | Eigen&Lanczos | Sound Eigen | Solid Eigen | Solid Axisym |