そして、せん断応力τ_xzとτ_yzもｘとｙ軸の回転により数値を変換しなければなりません。以下の方法で計算できます。回転した軸はプライムで表しています

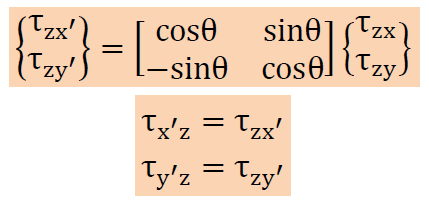
主応力τ_x'x'の方向を示す座標軸ベクトルも変換する必要があります。上のせん断応力と同様に以下のようになります。

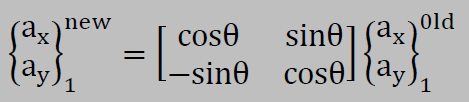
同様に他の2つの座標軸ベクトルも以下のように変換しなければなりません。

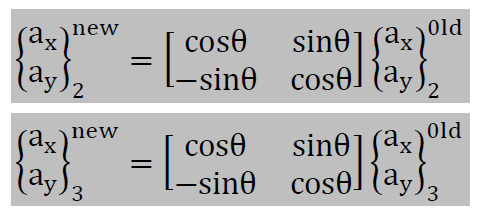
次のステップは、τ_x'zとτ_y'zの絶対値で大きい方を上で説明した方法で計算を進めます。このときτ_x'y'に再び数値が入るということに注意して下さい。このように2次元の面での軸の回転を逐次的に繰り返す演算を10回ほど繰り返すと真の値に限りなく近いτ_x'x'、τ _y'y'、τ _z'z'が計算されます。つまり、τ₁、τ ₂、τ ₃の主応力が得られたことになります。同時に、主応力の方向を示す座標軸のベクトルも同時に計算されます。

ところで上で説明した変換の方法ですが、複素数を使うと簡単に説明できます。まず、a_old=a_x+ia_yと置くと、a_new= a_olde^-iθで変換できます。座標軸をθ回転するということは、ベクトルを-θ回転し、xy軸間でそのベクトルを書くことと同じです。複素数の変数の掛算は回転を表します。つまり、z=iの場合、zは実軸から90度回転しています。そして、zz=iiはiにiを掛算するということは、更に90度回転させるということなので、zzは実軸の-1になります。このことから、i²=-1なります。これは、複素数の定義によく使われます。