上で説明した三次方程式の計算は、プログラムCUBICROOT.FORで行えます。使ってみて下さい。 主応力の座標軸を表すベクトル(固有ベクトル)は、Inverse Power法等で計算する必要があります。

■Jacobi法による主応力の計算■
この方法は、まず3つの主応力の方向を示す座標軸ベクトルを以下のように仮定しておきます。

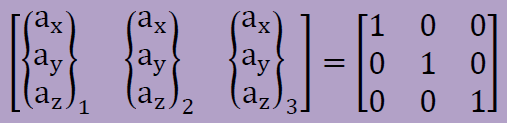
次にせん断応力の絶対値で一番大きい項を取り上げ、その項に関する2軸の間でそのせん断応力がゼロになるように座標軸を回転します。計算手順は、Mohr(モール)円と同じです。例えば、|τ_xy|がせん断応力の中で一番大きかったとします。するとτ_xyをゼロにするために必要な座標の回転角度θは、以下で計算できます。

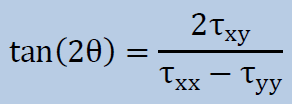
回転後の応力は、以下のように書けます。詳細については材料力学の主応力のところを学習して下さい。

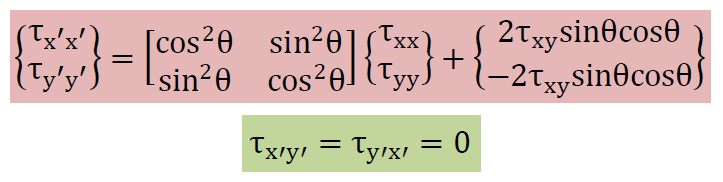
角度θですが、プログラムではarctan関数を使って計算することはありません。上の式からtan2θがわかっていますので、cos2θ=(τ_xx-τ_yy)/(2r)、sin2θ=τ_xy/r で定義できます。ここに、r=モールの円の半径です。そして、cos2θ=2cos²θ-1、sin2θ=2sinθcosθですから、座標の回転に必要なsinθとcosθは、以下で計算できます。

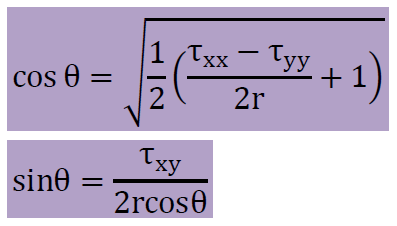
更に、モールの円を活用するとτ_x'x'とτ_y'y'は、下式に示すように簡単な形になってしまいます。