三重根で無い場合は、下の3次方程式を計算します。式は単純な形をしていますので、簡単に解の1つを得ることができます。例えば、Fortarnですと、ALPHA=BETA**(1.D0/3.D0)で計算できます。
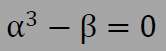
結果的に、主応力の1つはCardano法の手順により以下を得ることができます。
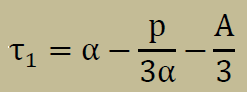
後2つの主応力は、上の3次方程式の残りの2つの解から得られます。未知数のαを3回掛算してβになる解は下図に示すように、半径がαの複素円上に有り、解は互いに2π/3の開きがあります。前にも言いましたが、複素数zを掛けるということは、掛けられた複素数(ベクトル)が複素面でzの持つ角度だけ回転するということです。この場合、2π/3回転します。
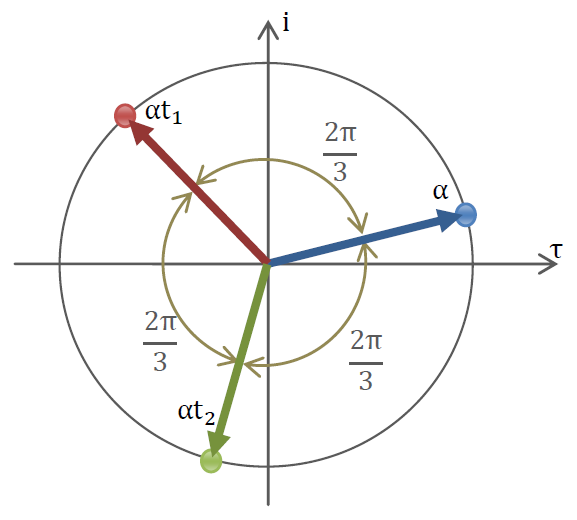
複素数の長さが1で、掛算される複素数を2π/3回転させる複素数は以下になります。上の図を参考にして下さい。ここで注意したいことは、αt2=αt12とも書けます。上図に示す3点を計算してくれるプログラムCM.FORが用意してありますのでプログラム中の複素変数zの数値を変えて計算してみて下さい。
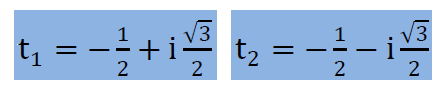
結果的に、3次方程式τi3 + Aτi2 + Bτi + C = 0の解は以下のようになります。
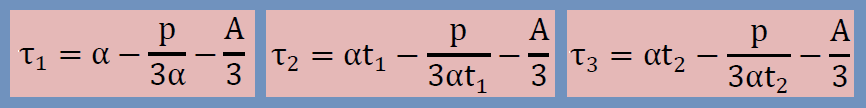
| BACK | NEXT |
|---|
| Menu | LU Decompo | Stiff | 3D Solid | 3D Fluid | Eigen&Lanczos | Sound Eigen | Solid Eigen | Solid Axisym |