ここに、上式のA, B, Cは以下のようになっています。

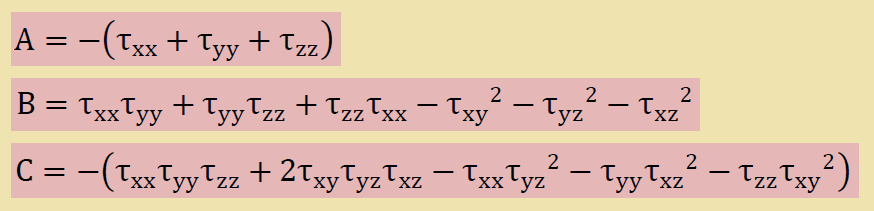
ここでは3次方程式の解法で良く知られたCardano法で主応力を計算してみましょう。この方法では、3次方程式に対し数回置き換えをします。すると、以下の2つの式が導き出されます。

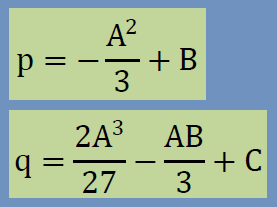
そして次の2次方程式を計算し、解としてβを得ます。

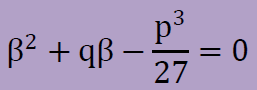
解は下に示すように2つ存在します。

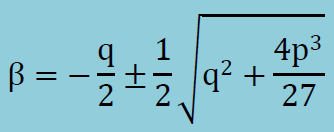
２つの内の1つを解とします。変数pがゼロの場合、上の2次方程式はβ²+qβ=0になり、βは、β=0またはβ=-qになります。この場合、β=0はtrivial solutionですのでβ=-qが2次方程式の解になります。そこで、p=0の場合を考慮するために、βとして以下を解にします。

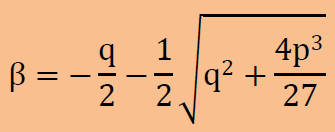
しかし、p=0とq=0が同時に起きる可能性があります。この場合、β=0となり、ここで話は終わりになってしまいます。では、どんな時にp=0とq=0が同時に起きてしまうのでしょうか。Cardano法を詳細に調べると、三重根 (Triple root)の時にpとqがゼロになってしまいます。例えば、λ=τ_xx=τ_yy=τ_zzそしてτ_xy=τ _xz=τ_yz=0の場合、主応力が三重根になります。計算をすると、A=3λ、B=3λ²、C=-λ³となり、これらはp=q=0を生産します。この場合、解はτ₁=τ₂=τ₃=A/3になります。プログラムを書くときには、この三重根を考慮に入れる必要があります。