したがって、領域積分は、次の様になります。
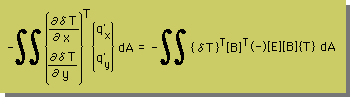
ここまでは、OKですか。理解できましたか。かなり詳しく説明してきましたので、理解できたと思いますが。
それでは、今まで学んだことをまとめてみましょう。次の式を、じっくり眺めてみて下さい。
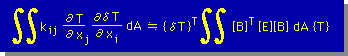
上の式は、かなり一般的に書かれています。要素の種類も限定されていません。上の式の形は、いたる所で出現しますので、しっかりと理解しておて下さい。
■三角形要素の場合■
上の結果と三角形要素をリンクしてみましょう。記述が大変になりますので、[E]を Isotropic にします。つまり、kij = kδij。
手始めに、三角形要素の[B]マトリックスを計算してみましょう。左下の様になるはずです。そして、[B]T[B]は、右下の様になります。チェックしてみて下さい。
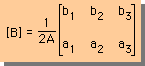 | 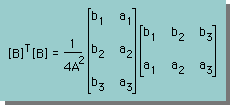 |
そして、[B]T[B]を三角形要素上で積分すると、下に示す様な対称マトリックスに成ります。

 |
 |
|---|
| BACK | NEXT |
|---|
| Menu | Heat Eq. | Cdtvty | WRM2 | Tri | Stiff | Bound | Ex | Rmk |