■入力データと計算方法■
ファイルWIRE0.DATは
ProgramWIRE3.FORのSUBROUTINE INPUTで取り込まれます。
そして SUBROUTINE INPUT を見ると次の様になっています。
| 行目 | 変数名 | 意 味 |
|---|---|---|
| 1 | NE | 要素数 |
| 2 | DOMAINL | 領域のx方向の全長 |
| 3 | WDENSITY | Wire の単位長さ当りの質量 |
| 4 | TXMAX, TXMIN, TXSTEP |
3つの実数があります。 これらが計算の手順を示しています。 微分方程式は非線形ですから z(x) の推測値が必要ですよね。 一番簡単なz(x)の推測値として両境界点を直線で結ぶ線が考えれます。 このとき Wire の Tension は無限大になりますよね。 そこで計算方法として まず 大きい値の Tx (TXMAX) と直線のguessのz(x)で解析を行い z(x)を得ます。 この場合、少ない繰り返し数で、解がえられます。 次のステップとして Tx から少し小さな値(TXSTEP)を引いて 計算されたばかりのz(x)を使って解析します。 この計算を Tx=TXMIN まで行います。 |
| 5 | Z1 | x=0 でのz座標値 |
| 6 | ZN | x=DOMAINL でのz座標値 |
Program WIRE3.FORを見ると他に幾つかの変数名が使われています。 以下にそれらの変数名と意味について書いておきました。 前ページと重複している物も有ります。
| Return 変数名 | 意味 |
|---|---|
| TX | x 座標軸方向の張力 |
| TZ | z 座標軸方向の張力 |
| SUMTZ | 節点1のTZと節点NNODEのTZ |
| WOW | GW*WL |
| GW | WDENSITY*GRAVITY=ワイヤーの密度と重力加速度との掛け算 WDENSITY*GRAVITY |
| WDENSITY | ワイヤーの密度 |
| GRAVITY | 重力加速度 |
| WL | ワイヤーの長さ |
| DEPTH | 両境界を結ぶ架空の直線から測定した垂れワイヤーの深さ |
| PARABOLIC | ワイヤーの垂れが2次曲線とした場合のz座標値 |
| TENSION | TS(I)の事でI節点を持つ両要素内の張力の平均 |
| TS-UP | 要素1内の張力 |
| TS-DW | 要素NE内の張力 |
| L-OF-WIRE | ワイヤーの長さ |
| W-OF-WIRE | ワイヤーの重量 |
| %ERROR | SUMTZとW-OF-WIREは同じになるはずですが その両者の誤差 |
| ITERATIONS | プログラム内で設定した誤差をクリアーするまでの繰り返し計算回数 |
次に入力データファイルのWIRE1.DATを見て下さい。 要素数=60、領域の水平方向の長さ=60cm、Wire の質量=0.3571428571429grams/cm、TXMAX,TXMIN,TXSTEP=20grams, 4.grams, 1.gram となっていますね。 プログラムの中で 重力は、1 としています。 境界条件は、Z1=0.,ZN=0. となっていますね。
■計算例と実測■
 |
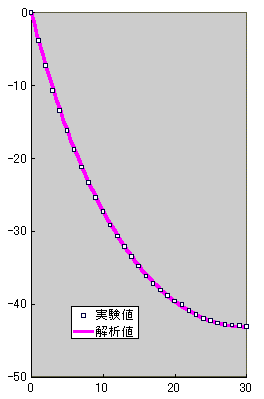
この手の実験は簡単ですので やってみることにしました。 上で説明した材料は ホームセンター等で買える chain です。 全長=112cm、全質量=40grams でした。 壁に長さ60cmの水平線を描き線の両端にchainの両端を画鋲で吊るしました。 すると最初のページで紹介した様に chainは曲線を描きます。 この実験では chain の最大深さは、約43cmになりました。 この様な状況を実現するには Tx=5.228grams になっていることが 計算からわかりました。 このときの結果を下図に示します。計算結果の半分を表示しています。 実験と計算結果は よく一致していますね。 計算には上のデータと同じWIRE1.DATを使いました。 図をクリックするとExcelで書かれた実験結果が得られます。 |