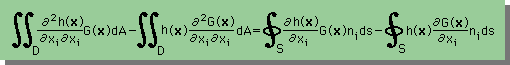
上式の左辺は、領域積分になっていて、右辺は境界積分で構成されています。つまり、上式はDivergenceの定理の副産物であることが分かります。そして、この式をGreen's Second Identity と言います。この式が境界要素法のベースになっていますので、しっかり理解しておいて下さい。

■Kernel function■
問題は、”Green's Second Identity をどう使うか”です。まず、定常のHeat equation や定常のGroundwater の式の様に L(h(x)) = 0 である場合を考えてみましょう。すると、Green's Second Identity は、次の様になります。

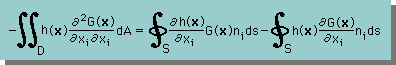
このままでは、まだ何の役にも立ちません。つまり、関数 G(x) が明確にならない限りh(x) を計算できません。多分 G. Green もここで関数 G(x) について様々なアイデアを出したにちがいありません。

G. Greenは、関数 G(x) に2次元Laplace eq. を満足するGreen's function を提案しました。下式がそうです。

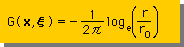
ここに、r=|x-ξ| です。r₀ は、基準距離です(例えば r₀=1)。 距離 r を r₀ で割っている理由は、関数 log の引数を無次元にしたいからです。関数 G(x,ξ) の値は、x=ξ(ξ=(ξ_x,ξ_y)) の位置で正の無限大になります。この点のことを singular point とか source point とか言います。ここでは、 source point で統一しましょう。このように、他の数値計算方法と違って、境界要素法では、 source point からの影響を積分を行う点で観察するという考えのもとで、アルゴリズムが出来上がっています。観察し積分を行う点(x)のことをobservation point といいます。ですからh(x)を計算したい点をsource pointとし、境界上をobservation point とし境界積分を行うと、h(ξ)が得られることになります。なんとなく分かったようで分からない感じだと思います。後で詳しく説明しますので心配しないで下さい。今の時点では、境界要素法に source point が存在しているということを理解しておいて下さい。

位置 ξ と(x)の詳細については、次のページの図を参照して下さい。