ところで、前ページの積分式に話しをもどします。境界要素法の積分式を導くためには、Divergence の定理を2回、積分式に施す必要がありました。前ページの積分式の場合は、次の様になります。

ここに、qn(x) は、下の様に定義されていました。
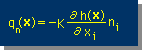
そして、上の積分式の I をδhi で微分してゼロと置くと、下の Source point i での積分式が出来上がります。

上の式は、私達が以前、導き出した境界要素法の積分式と同じです。
■直接法■
ここで紹介している方法を、境界要素法の中では、直接法といいます。直接法では、このページのトップにある積分式がキーになっています。この式の中には、非常によく似た2つのシステムが混在しています。
| 温度 h(x) と qn(x) のペアーのシステム |
| Kernel function からなるG(x,ξ)=δh(x,ξ) と F(x,ξ)=δq(x,ξ) のペアーのシステム |
つまり、2番目のシステム(δh(x,ξ) と δq(x,ξ) ) が得られると、境界要素法の積分式を簡単に導くことができます。Laplace 方程式の場合、下の2つがGとFの式になります。
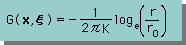 |
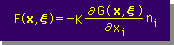 |
| BACK | NEXT - Discretization |
|---|
| Menu | Fundamentals | Formulation | discretizatione | Example | Straight | Multi-D |