そして、未知数としては、qn1、h2、qn3、h4 が残り、連立方程式は下に示す様に簡略化されます。つまり、[A]{X}={RHS}です。
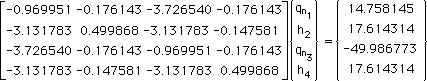 |
有限要素法の剛性マトリックスと違い、非対称で、対角要素もさほど強くありません。連立方程式を解くには、悪い条件が揃い過ぎていますね。とりあえず、上の連立方程式を解くと、次の結果が得られます。
| qn1 | 11.74366 |
| h2 | 50.00000 |
| qn3 | -11.74366 |
| h4 | 50.00000 |
要素の2と4上では、温度が50になっています。これは、要素上の平均温度として考えられますので、計算結果は、good です。しかし、qn1 は、10 が厳密解ですから、約2割の誤差があります。この誤差は、要素2と4上で温度を一定としたことが、原因になっています。Linear 要素を使うと、この誤差は消えます。
ここまでは理解できましたか。とにかく計算手順が理解できていればOKです。手計算で全てが出来れば尚OKです。しかし、計算が複雑ですのでプログラミングで計算できる様になっておいて下さい。プログラミング言語は問いませんので。
| BACK | NEXT |
|---|
| Menu | Fundamentals | Formulation | discretizatione | Example | Straight | Multi-D |