■Source point(ξi) を含む要素上での積分■
これまでの説明は、Source point (ξi) と積分点 (x) の距離(r) が常にゼロ以上の場合でした。ここでは、積分区間にξi が存在している場合を考えてみましょう。つまり、r=0を含む積分です。まず、下図を見て下さい。
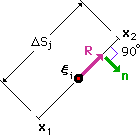 |
Source point (ξi) がconstant element の中央に位置しています。 距離(r)を示すベクトルRは、normal ベクトルn に対し90度をなすことになります。つまり、R・n=0 になります。結果的に、Fii の計算の場合、Source point(ξi) を含む要素上では、次のことが言えます。
| Fii=0 |
では、G(x,ξ) の積分は、どうなるでしょう。G(x,ξ) は、距離(r)の関数ですから、Source point(ξi) を含む要素上では、下図の様な値を示します。グラフの横軸は、距離(r)です。
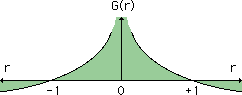 |
着色された部分を積分することになります。G(r) は、r=0 で無限大になります。しかし、loge(x) の0からaまでの定積分は、下の様になります。
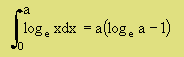
ですから、r=0 を含むG(r) の積分は、有限値になります。したがって、G(r) の積分は、下式により厳密に計算できます。
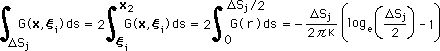 |
| BACK | NEXT |
|---|
| Menu | Fundamentals | Formulation | discretizatione | Example | Straight | Multi-D |