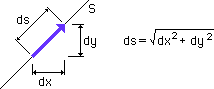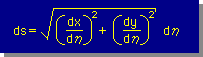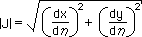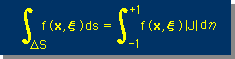Two Dimensional Boundary Element Method
Discretization by Constant Element-5
■座標変換■
では、早速、GijとFij の計算を行って見ましょう。
Constant element の場合、GijとFij の内容が簡単ですので、厳密に積分を行うことができますが、
ここではGauss-Legendre法 の数値積分法での計算方法を紹介します。
そこで、計算の前に準備しなくてはならないのが座標変換です。まず、下図を見て下さい。
x座標とy座標が、無次元座標ηへ変換されています。つまり、x=x(η) そして y=y(η) ということになります。
このことから x と y の全微分は、次の様になります。
 また、下図の左に示すように、境界の線分ds(x,y) は、ds2=dx2+dy2です。
また、下図の左に示すように、境界の線分ds(x,y) は、ds2=dx2+dy2です。
ですから、無次元座標値の関数としてのds(η)は、下図の様になります。
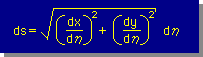 解析学では、下式が一般に使われます。
ここに、|J| は、Jacobian matrix の Determinant です。2次元では、J はスカラーです。
解析学では、下式が一般に使われます。
ここに、|J| は、Jacobian matrix の Determinant です。2次元では、J はスカラーです。
これまでを総合すると、実座標系の関数 f(x,ξ) の積分は、下式の様に無次元座標に変換することができます。
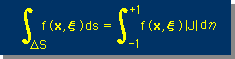
BACK
NEXT
Menu
Fundamentals
Formulation
discretizatione
Example
Straight
Multi-D