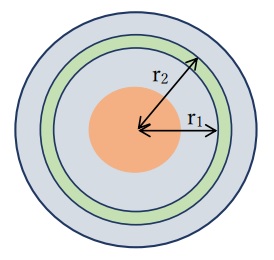
■分布電荷qが存在するポアソン方程式を有限要素法で解く方法■
芯線に分布電荷qが与えられている状態を有限要素法で解いてみます。
この解析で得られることは、芯線の中心での電位Vおよび磁気ベクトルポテンシャルAzの値です。
集中電荷の解析から分かっていることですが、r=aからr=bの間は、
分布電荷qを与えた解析とGauss's Lawを芯線表面に与えたときとでは同じ結果になります。
この辺も両者の計算結果を比較して、同じになることを示してみます。
式の展開の詳細については、有限要素法のページを参考にして頂くとして、まず、有限要素法は、
以下の積分式からスタートします。
ここで紹介している手法は、有限要素法の中の重み付け残差法という基本的な方法です。
| \begin{eqnarray} \int_{0}^{2\pi}\int_{r_1}^{r_2}\left(\frac{d}{dr}\left(r\frac{dV}{dr}\right)+ \frac{q(r)}{\varepsilon}\right)\delta Vrd\theta dr=R(\delta V) \end{eqnarray} |
| \begin{eqnarray} \frac{\partial R}{\partial\delta V}=0 \end{eqnarray} |