Coaxial19

Electromagnetics and Ham Radio
Coaxial19

■Hybrid要素の計算結果■
要素数をかえながら前回と同じ問題を解いてみました。参考までに繰り返しになりますが計算で用いた数値は、a=6.35, b=9.5, c=12です。要素数は、20、40、80、160です。下の図は、節点13～17までをプロットしてあります。データ作成には、 SETHYBRID-OUTER-RECTANGULAR-QUARTER.FOR を使いました。計算には、BEM8MIXQ.FORを使いました。

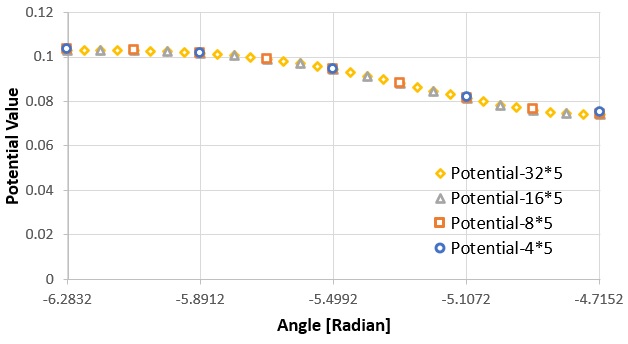下の表は節点13～17までのポテンシャルの平均値です。要素数が640の計算結果を誤差ゼロとした場合、要素数20でも誤差は0.277866%になっています。かなり良い解析精度になっています。

要素数	Potential	誤差(%)
20	0.091263	0.277866
40	0.091274	0.265776
80	0.09138	0.150013
160	0.091454	0.069298
640	0.091517	0

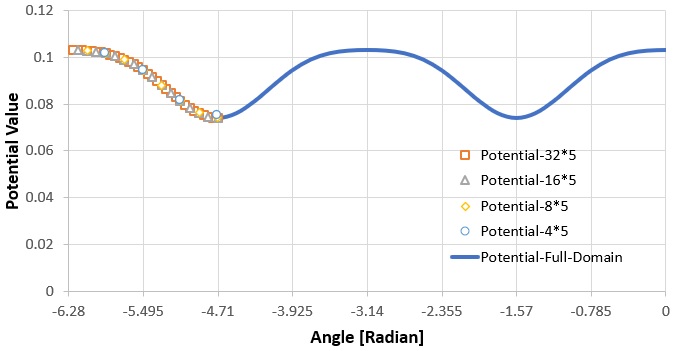
下は、上の計算結果とフル計算領域の結果とを比較してみました。

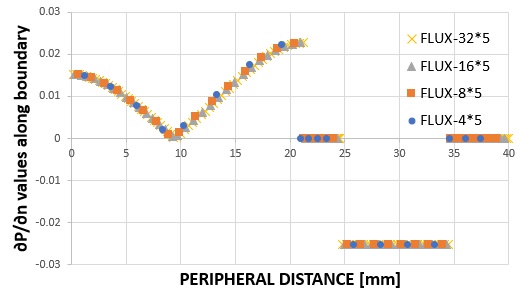
下のグラフは、境界上の∂P/∂nです。横軸は周長で起点は節点1です。方向は半時計方向になっています。上の要素分割図で説明すると、周長が0mmの点が節点1、9.5mmが節点5、21.5mmが節点9の位置です。

下の図は、周長21.5mmまでを他の計算結果と比較してあります。青丸●が今回の計算結果、四角■が角問題の処理なしの2次要素、そして、青の線－がフル領域で計算した結果です。

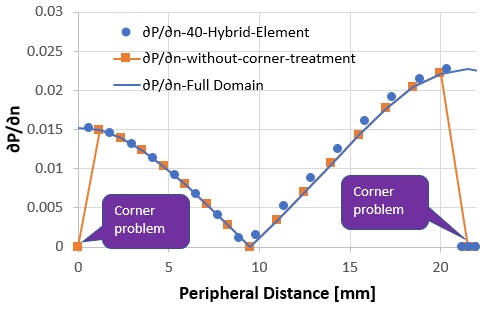角問題の処理なしでも要素が2次だと、今回の問題に限ってだと思いますが、全般的に計算精度は良さそうです。しかし、角問題を起こしている位置が製品の設計に重要だとすれば、角問題を起こさないHybrid要素は有効な計算手段と考えて良いでしょう。

Preceding Page Preceding Page

Menu Inductance Capacitance Z₀ Exp Balun Coaxial Off center fed DP Helmholtz FEM BEM Internet College of Finite Element Method