| \begin{eqnarray} f_1=\frac{1}{\pi}{log}_e\left(\frac{D}{a}\right) \end{eqnarray} | \begin{eqnarray} f_2=\frac{1}{\pi}{log}_e\left(\frac{D}{a}+\frac{1}{4}\right) \end{eqnarray} | \begin{eqnarray} f_7=\frac{1}{\pi}{log}_e\left(\frac{D}{a}-1\right) \end{eqnarray} |
| \begin{eqnarray} f_{Pmax}=\frac{1}{\pi}{log}_e\left(1.6208\left(\frac{D}{a}\right)+0.3083\right) \end{eqnarray} |
| \begin{eqnarray} f_3=\frac{1}{\pi}{log}_e\left(\frac{D}{2a}+\sqrt{\left(\frac{D}{2a}\right)^2-1}\right) \end{eqnarray} | または | \begin{eqnarray} f_3=\frac{1}{\pi}{log}_e\left(\frac{D}{2a}+\sqrt{ \left(\frac{D}{2a}-1\right) \left(\frac{D}{2a}+1\right) } \right) \end{eqnarray} |
| \begin{eqnarray} f_{new}=\frac{1}{\pi}\left(0.3{exp}\left(-0.25\left(\frac{D}{2a}-1\right)\right)+ {log}_e\left(\frac{D}{2a}+\sqrt{ \left(\frac{D}{2a}-1\right) \left(\frac{D}{2a}+1\right) } \right)\right) \end{eqnarray} |
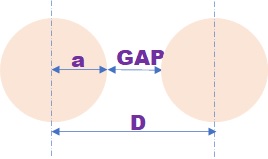
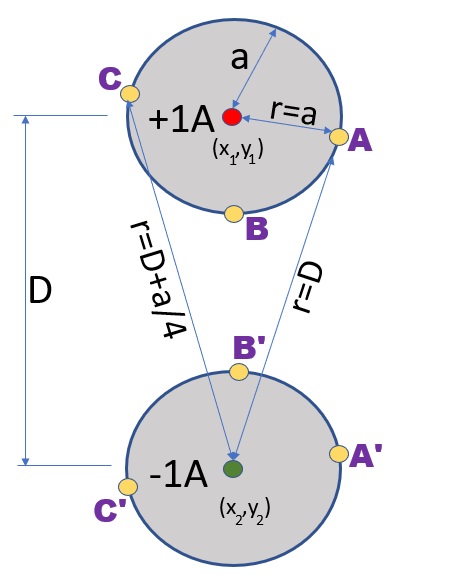
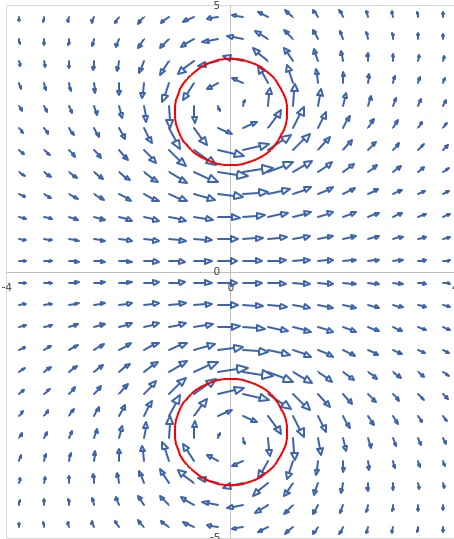
これらの上式はペアー導線の周辺で観測したときに得られました。 f1は下の図の点A、f2は点C、f7は点C、fpmaxは導線の中心付近でした。 下のベクトルプロットの渦の中心がその点です。f3は導線表面の電位(V)および磁気ベクトルポテンシャル(Az)が一定という条件で得られました。 最後のfnewはインダクタンスの実験結果をベースに得られた実験式で理論的な背景は有りません。