■計算結果と要素数の関係■
導線の断面を要素で分割する場合、計算精度が問題になります。 そこで、要素数を徐々に増加してゆき、電位の変化をみました。下図にその結果を示します。

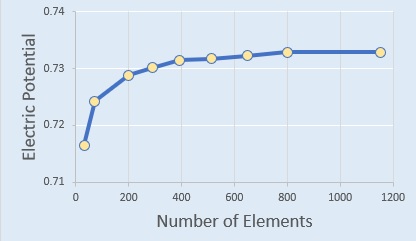
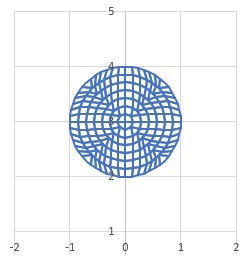
要素数が400位(392)で電位の値は落ち着いているようです。 上図のグラフの最初の点の要素数は32(導線当たりは16です)です。次の点の要素数は72(導線当たりは36です)です。 電位の増加量は1%ですので、要素数32でも十分な結果が得られると考えてよいと思います。 安全のため今後の計算は、要素数392(導線当たりは186です)で行います。下に要素数が392の場合の 要素分割の状況を以下(左側)に示します。
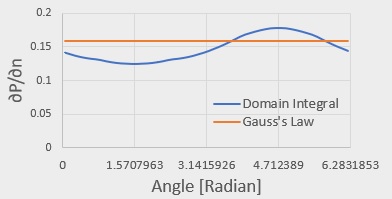
要素数392で導線の表面で∂P/∂nを計算すると、以下(右側)になります。結果に改善がみられます。 したがって、導線の表面の少し離れた位置でGauss's Lawが再現されていると思われます。