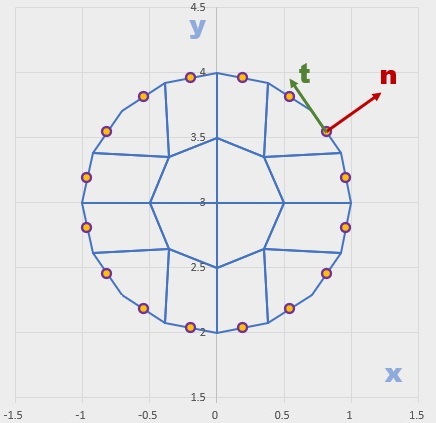
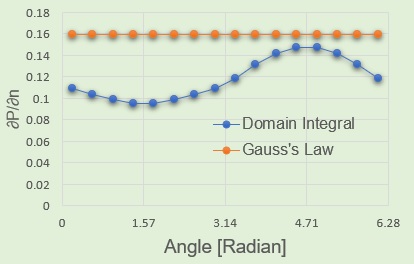
橙色の線がGauss's Lawによる値(D=Q/(2πR)=0.159)で、青色の線が今回の境界要素法での電束密度の結果です。 導線の下側つまり、ペアのもう1つの導線に近い側(πから2π)ではGauss's Lawの値に近いですが、 導線の上側(0～π)ではGauss's Lawの値より低くなっています。傾向的には、矛盾の無い結果と考えてよいと思いますが、値そのものが小さいです。 しかし計算結果からGauss's Lawで電荷を計算すると、Q=0.789でした。Q=1であるべきであるのですが、１つ考えられる理由として、 要素の数があげられます。要素数を増やすと、電荷はQ=1に近づくはずです。要素数が少ないために、導線の断面で電荷が適切に等分布状態になっていないと 考えられます。電荷が導線の中心に集中していると考え、導線の表面から少し離れた円周上で電束密度とGauss's Lawを比較すれば 境界要素法での計算結果の妥当性が判断できると思います。