前ページでも説明しましたが、τxx、τyy、τzzをNormal Stressと言い、部材が引き伸ばされる応力の方向をプラス、圧縮される方向をマイナスとしています。
τijのNormal Stress以外(つまり、残り6つ)をShear Stressといいます。このストレスについて、ΣMi=0(非常に小さなキューブだから=0になる)を施すと、次の様になります。
| τxy=τyx | τxz=τzx | τyz=τzy |
このことから、ストレス tensor は、対称であることが分かります。Shear Stressのプラス/マイナスも、前ページの説明の通りですが、応力の方向と物の変形を図で示すと次の様になります。
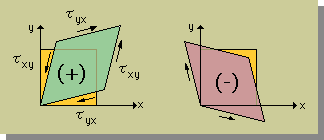
つまり、座標軸の原点に接している物の内角が、90度以下になるように働く応力がプラスで、90度以上がマイナスになります。
これまで議論してきた力のバランスを微分のかたちで表すと、応力解析の支配方程式、つまり Navier Equations を導くことができる。支配方程式については、後程Cauchy's Formulae を用いて詳しく説明しますので、ここでは説明をカットします。
■主応力(Principal Stresses)■
FEM解析等で計算され応力(ポスト処理で変位から求める)は、事前に決められた座標系が基準になっています。つまり、座標軸のオリエンテーションが変われば応力の値も変化することになります。
しかし、物体内および表面に発生している応力は、座標軸に関係なく存在しています。したがって、物体にダメージを与えようとしている最悪の応力を知る必要があります。この最悪の応力を主応力(Principal Stresses)と言います。そして、この主応力は、座標軸を回転して得られる最大最小の応力のことです。
ここでは、最大最小Normal Stresses の算出方法を学びます。
| BACK | NEXT |
|---|
| Menu | Basics | Material | τ-ε | Failure | Navier | 3dim | 2dim | Sample |