最終的に出来上がるグローバル剛性マトリクス[B]T[D][B]の積分は、対称になっています。ですから、半分のみ保存すればよいことになります。ですからグローバル剛性マトリクスを半バンドマトリクスとして保存することにします。すると、SK(I,J,K,L)は、グローバル剛性マトリクス[AM]に下の表に示すようにassembleすればよいことになります。ます要素のK節点に対応したグローバル節点をiとしておきます。そして要素のL節点に対応したグローバル節点からiを差し引き1を加算した値をjとしておきます。
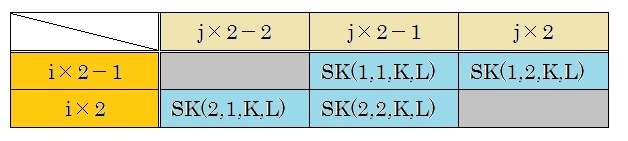
ただし条件としてj×2-2>0, j×2>0でなければなりません。これをFortranプログラムで書くと以下になります。
DO K = 1 , ND
I = NODEX(IEL,K)
II = I*2
DO L = 1 , ND
J = NODEX(IEL,L) - I + 1
JJ = 2*J
M = M + 1
IF ( J .GT. 0 ) THEN
AM(II-1,JJ-1) = AM(II-1,JJ-1) + SK(1,1,K,L)
AM(II ,JJ-1) = AM(II ,JJ-1) + SK(2,2,K,L)
AM(II-1,JJ ) = AM(II-1,JJ ) + SK(1,2,K,L)
IF ( JJ-2 .GT. 0 ) THEN
AM(II ,JJ-2) = AM(II ,JJ-2) + SK(2,1,K,L)
END IF
END IF
END DO
END DO
以上の事柄を全ての要素について行うと、グローバル剛性マトリクス[AM]が完成します。
| BACK | NEXT-Sample |
|---|
| Menu | Basics | Material | τ-ε | Failure | Navier | 3dim | 2dim | Sample |