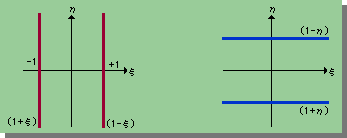
そして残りの節点11, 12, 2, 3でゼロに関数を探さなければなりません。それは下図に表す円の式で 成し遂げることができます。
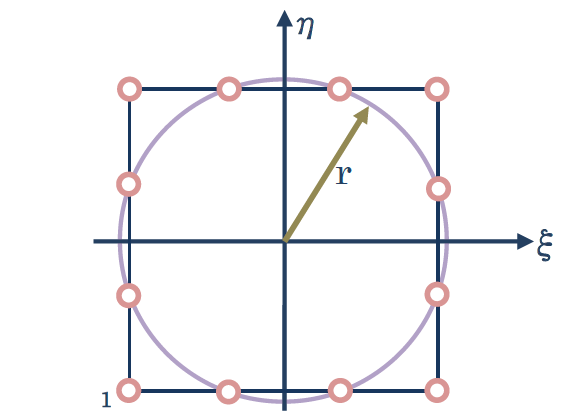
円の半径rは、r2=12+(1/3)2です。つまり、 r2=10/9になります。 ですから、円の式によるゼロ関数は、 ξ2+η2-10/9または、9(ξ2+η2)-10で上図の円上で ゼロになります。するとN1(ξ,η)の形状関数は以下になります。
座標の(ξ,η)=(-1,-1)でN1(ξ,η)=1になるようにaを決定すれば形状関数が出来上がります。 計算すると、a=1/32になります。
■N2(ξ,η)
次に形状関数のN2(ξ,η)はどうなるでしょう。節点3を除けば、ゼロ関数は上上図を参考にすると(1+ξ)(1-ξ)(1-η)ですね。そして節点3のゼロ関数は下図に示すようにξが+1/3でゼロになればよいので、(1-3ξ)ですね。
| BACK | NEXT |
|---|
| Menu | 4-noded | Create | 8-noded | 9-noded | 12-noded | 3-Dim | Example | Helmholtz |