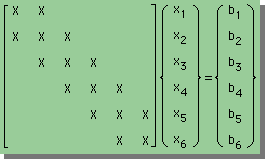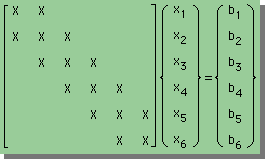Numerical Method & Algebla
Simultaneous Equations-4
■その1: Tri-Diagonal Matrix■
有限要素法では出来上がった連立方程式のマトリックスがBanded Matrixになることが多い。
つまりマトリックスの対角要素付近に数値が現われ対角要素から遠い部分はゼロに成っています。
まずTri-Diagonal Matrix について説明します。
下に典型的なTri-Diagonal Matrixを持つ連立方程式を示します。
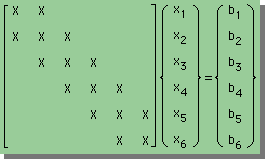対角要素の両隣に1本づつ筋が走っているように値がつまっていて その他はゼロになっています。
この様にゼロの為にをメモリー確保するのは無駄になってしまいます。
そこでマトリックスを次のように立てます。
マトリックスを この様にコンパクトにすると計算に必要なメモリーを大幅に削減できます。
前に紹介したGaussの消去法では、n×n であるのに対し この場合 n×3で解析が可能になります。
下に上図のようにコンパクト化したTri-Diagonal Matrixの連立方程式をGaussの消去法で解くSub Programを紹介します。
Program名をクリックするとソースが表示されます。
| Sub Programの名称 | TRIDIA |
|---|
| 変数：MXN | メモリー確保のためのマトリックスサイズの最大値 |
|---|
| 変数：NNODE | 計算に用いるマトリックスのスサイズ |
|---|
| 変数：A | マトリック [A]=[aij] |
|---|
| 変数：B | 連立方程式の右辺。説明の{B}と同じ。 |
|---|
マトリックスのサイズがA(MXN,3)であることに注意して下さい。
BACK
NEXT
Menu
Integral
Derivative
Matrix
Simultaneous
Internet College of Finite Element Method