---

Numerical Method & Algebla
Simultaneous Equations-3

---

次に3X3のマトリックスをもつ連立方程式を解いてみましょう。

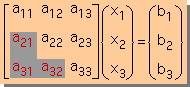2x2同様、上のa₂₁=a₃₁=a₃₂=0であると、x₃=b₃/a₃₃で計算でき、x₂とx₃もBack substitutionにより求めることが出来ます。 説明のために上式を次の様に書き直します。

a11x1	+	a12x2	+	a13x3	=	b1	..........Eq.1
a21x1	+	a22x2	+	a23x3	=	b2	..........Eq.2
a31x1	+	a32x2	+	a33x3	=	b3	..........Eq.3

まずGaussの消去法を用いて a₂₁とa₃₁をゼロにすることを行います。 そのために -(a₂₁*Eq.1)/a₁₁をEq.2へ、-(a₃₁*Eq.1)/a₁₁をEq.3へ、それぞれ加えます。 すると

a11x1	+	a12x2	+	a13x3	=	b1	..........Eq.1
		a22x2	+	a23x3	=	b2	..........Eq.2
		a32x2	+	a33x3	=	b3	..........Eq.3

上式の緑色で示してある部分は、以前の値とは違うことを意味します。 次に行う作業は、2x2の時とまったく同じです。 つまり -(a₃₂*Eq.2)/a₂₂をEq.3へ加えます。 すると連立方程式は次のように成ります。

a11x1	+	a12x2	+	a13x3	=	b1	..........Eq.1
		a22x2	+	a23x3	=	b2	..........Eq.2
				a33x3	=	b3	..........Eq.3

よって x₃=b₃/a₃₃となり x₂とx₁もBack substitutionにより計算出来ます。 さらに、4x4やnxnの連立方程式も、同様なテクニックで計算できます。 ここで説明したGaussの消去法のSub Programを紹介します。 Program名をクリックするとソースが表示されます。

Sub Programの名称	SYSTEM
変数：MXN	メモリー確保のためのマトリックスサイズの最大値
変数：N	計算に用いるマトリックスのサイズ
変数：A	マトリックス [A]=[aij]
変数：C	連立方程式の右辺。説明の{B}と同じ。

---

BACK NEXT

---

Menu Integral Derivative Matrix Simultaneous Internet College of Finite Element Method