■マトリックス型有限要素式■
これまでに、積分式の各項を離散化してきました。次のステップは、それらの項を1つにまとめることです。下式が1つにまとめたマトリックス型積分式です。

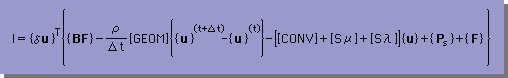
さらに、∂I/∂{δu}=0を計算すると、下の{u}を未知数とするマトリックス型有限要素式が出来上がります。

上式の{BF}+{P_s}+{F}は、便宜上、時間的に変化しないものとします。すると、上式にCrank-Nicolson法を適用する項は、{u}のみになります。ここでプログラミング時に、留意してもらいたいことに、[CONV]は{u}^(t+Δt)の関数であるということがあります。つまり、繰り返し計算が、必要であるということです。

■Reduced Integration Technique■
もう1つ留意してもらいたいことが有ります。それは、λdivV項の積分です。第2粘性係数(λ)による応力と粘性係数(μ)による応力を区別するために、λdivVの項は、他の項のGauss積分精度よりも、1ランク低い積分精度で計算します。この方法を、Reduced Integration Procedure といいます。

もう少し具体的に説明します。有限要素法では、各時間ステップに、1つのGlobal matrix と定数項(Right hand side)が生成されます。このGlobal matrixには、微分方程式の{u}に関係する項の積分結果が数値として集約されています。そして、連立方程式を解くと、計算結果には、微分方程式の各項の効果がはっきりと現われています。例を上げると、微分方程式には、{u}に関係する2階微分の項、1階微分の項、そして生成項がありますが、それぞれの特徴が計算結果に現われてきます。しかし、2階微分の項(複数)の1つを別扱いにしたい場合、他の2階微分の項と同じGauss積分手順では、目的を達成出来ません。実際にλ項を他項と同様に正規のGauss積分で計算すると、粘性のかなり効いた計算結果になってしまいます。

そこで、特別扱いしたい項のGauss積分を、正規よりも1ランク低い積分精度で計算します。すると、まったく別ものが出来上がります。大げさに言うと、2階微分の項と生成項の違い位の結果になります。厳密的には、積分精度を低下しても、divVそのものの性質は、変りません。しかし、要素の振動モードの数または共振周波数の数が変化します。これについては、弾性体の固有振動解析に低減精度積分を用いた場合を参考にして下さい。