■Time Derivative Terms■
時間項の処理については、既に学習しましたので、ここでは、結果のみを紹介します。時間微分に差分法を適応すると、時間項の積分は、次の様になります。

時間項では、下のショートハンドノーテーションを使います。前にも紹介しましたが、[GEOM]は、要素の形状的な特徴を表すということから、Geometric matrix と呼ばれます。そして、[GEOM]には、lumping を施します。
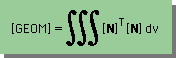
■Bounadry Integral■
流体解析では、境界積分項を計算することは、ほとんどありません。流体解析でよく遭遇する境界条件は、
等が、上げられます。どれをとっても、境界積分の計算は不要であることが理解出来ると思います。理解できない方は、もう一度、1次元と2次元FEMを復習して下さい。
したがって、ここでは一応、下に示す様に、弾性解析と同じ記号を用いることにします。
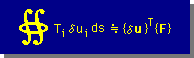
| BACK | NEXT |
|---|
| Menu | Govern | FEM | 2nd Visco | DCF | Cylinder | /Heat | Lub |