支配方程式が出来上がりましたので、早速、有限要素式を導くことにしましょう。 流体解析の有限要素式を導く手順は、弾性解析の時に学んだ事柄が、そのまま流用できます。したがって、先へ進む前に、3次元弾性解析の有限要素式を復習なさることを、お奨めいたします。

■WRM■
残差を定義し、積分式を設定するところから始めましょう。これまでに学習したWRMの手順に従うと、流体の運動方程式の積分式は、次の様になります。

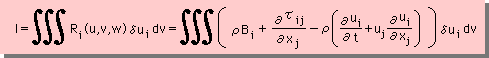
次の作業は、τ_ijの積分に対して、部分積分を施します。すると、下式の様になります。ここまでは、問題なく理解できたと思います。

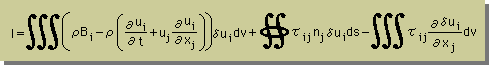
ここまでで、弾性解析との違いは、未知数が変位から速度になり、Convective terms が追加されたことです。それに、座標系は違います。しかし、プログラムを作成する上での違いは、少ないことに気付くと思います。実際、私は、流体力学のプログラムを先に作成し、その後、時間項とConvective terms をプログラムから削り取り、弾性解析のプログラムにしました。

■応力の式のマトリックス化■
流体の応力の考え方は、弾性力学のそれと比べると、違いますが、有限要素式を作り上げる手順からみれば、殆ど同じです。違いと言えば、λdivV の取り扱いです。流体では、応力を次のマトリックス式で表すことにします。

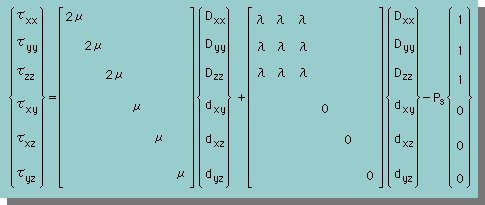
ここに、d_ij=2D_ijです。