■概要■
運動方程式とHeat Equation を連立に解くことが出来ると、様々な自然現象をコンピューター上で再現できます。例えば、流体を加熱することによる上昇気流があります。ここでは、コンテイナーに入っている摂氏4度の水を、コンテイナーの側面および底面から、加熱および冷却した場合の水の動きを解析してみます。
■水の温度特性■
水には、他の流体にない不思議な温度特性が有ります。それは、大気圧下において、水は摂氏4度で最大密度になることが知られています。
しかし、最大密度のなる理由については、まだ解明されていません。密度測定の実験によると、密度分布は、摂氏4度を境に対称になっているとされています。したがって、数値計算上では、密度が摂氏4度でピークになる、2次曲線で近似することが出来ます。数値解析に、最も頻繁に使われる水の密度の式を下に示します。図中の式は、水の温度が摂氏0度から摂氏8度までの範囲で、有効であるということに注意して下さい。
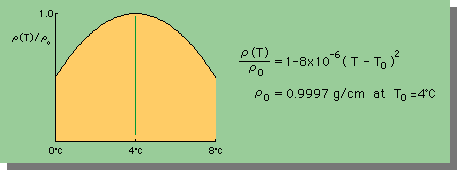
その他、摂氏4度付近の水のKinematic Viscoaity (粘性係数/密度)と熱伝導係数を下に示します。ともに大気圧下での値です。
| 項目 | 単位 | 式の意味 | 式 |
|---|---|---|---|
| 粘性係数 | cm2/sec | 粘性係数/密度 | μ/ρ0=ν=1.22x10-5T2-5.99x10-4T+0.01787 |
| 熱伝導係数 | cm2/sec | 熱伝導係数/(比熱*密度) | k=κ/(ρ0Cp0)=1.4x10-8T2+4.7x10-6T+0.001339 |
ここでは、粘性係数や熱伝導係数を定数とした場合の計算結果も紹介します。
| BACK to Flow around Cylinder | NEXT |
|---|
| Menu | Govern | FEM | 2nd Visco | DCF | Cylinder | /Heat | Lub |