上式を見ると、μの項とλの項が、分離されています。理由は、数値計算上で、μとλの効果を別々に引き出したいからです。μとλを1つのマトリックスで表すと、τxxは、下式の様になります。
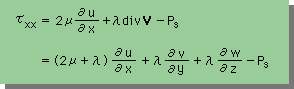
つまり、2μ+λ の粘性の解析を行うことになります。このままでは、μを変えたのか、λを変えたのか区別がつかなくなります。のちほど、μとλを数値計算上で分離する方法を、数値積分のところで紹介します。
話しを応力の式に戻します。弾性解析と同様に、応力の式を次のショートハンドで書くことができます。
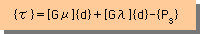
上の応力は、有限要素法と関係なく成立する式です。しかし、上式の{d}ベクトルを計算するためには、要素を決める必要があります。つまり、ここで初めて、応力{τ}が近似解になります。ここでは、節点数が8個の6面体要素を使います。したがって、u(x,y,z,t)≒[N]{u}、v(x,y,z,t)≒[N]{v}、w(x,y,z,t)≒[N]{w}で近似できます。そして、{d}ベクトルも、次の様に近似できます。
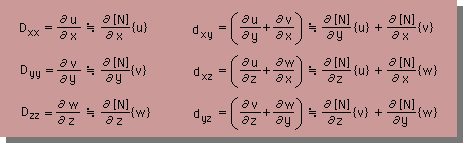
| BACK | NEXT |
|---|
| Menu | Govern | FEM | 2nd Visco | DCF | Cylinder | /Heat | Lub |