形状関数の微分については、弾性解析を参考にして下さい。
すると、{d}ベクトルは、次の[B]マトリックスと{u}ベクトルとの積で、書くことができます。
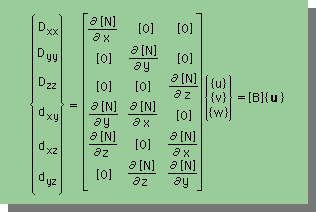
結果的に、流体の応力は、次のショートハンドで書き表すことができます。
| {τ}≒[Gμ][B]{u}+[Gλ][B]{u}-{Ps} |
■Stiffness terms■
次に、積分式の一番右の項が、どの様に近似できるか考えてみよう。この項についての詳細は、弾性解析で説明しましたので、ここでは、概略を表示します。
まず、積分される内容のIndex notation を通常のxyzで書きます。 τxy=τyx、τxz=τzx、τyz=τzyであることを考慮し、少し並べ換えると、次の様になる。
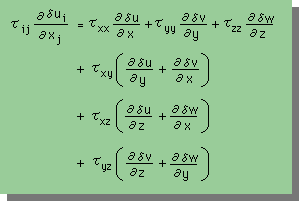
| BACK | NEXT |
|---|
| Menu | Govern | FEM | 2nd Visco | DCF | Cylinder | /Heat | Lub |