上の式の右辺を見ると、2つのベクトルの積になっています。つまり、{τ}^T{δd}で示すことができます。そして、{δd}は、下式に示すように書けます。

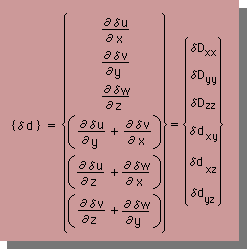
ここに、δu=[N]{δu}、δv=[N]{δv}、δw=[N]{δw} です。

すると、{δd}=[B]{δu}になりますね。理解できない人は、弾性解析のところを復習してくださいね。

これまでの事柄をまとめると、次の近似が成り立ちます。

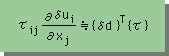
結果的に、積分式の一番右の項は、次の様に近似できます。

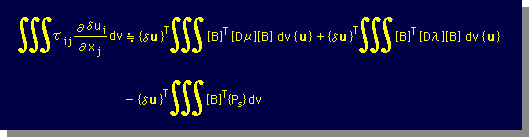
上式の静圧力の項は、Body force の項とでキャンセルされるため、ここでは、静圧力項について、これ以上の説明はしません。

ここまでは、弾性解析とほぼ同じですので、理解に苦しむことはないと思いますが。とりあえず、ここまで理解できましたら、小休憩を取ってください。ところで、式がだんだん長くなってきましたので、上式に関し、次のショートハンドノーテーションを使うことにします。