■Convective terms■
流体解析には、Convective terms が有ります。この項の数値的処理に一工夫が必要になります。理由は、(1)Convective termsは非線形、(2)出来上がるマトリックスが非対称、があるからです。さらに、有限要素法の大きな特徴であるグローバルマトリックスの対称性が崩れることになります。

とりあえず、下のConvective terms の近似式を求めることにしましょう。 密度(ρ)は、要素内の平均値とします。

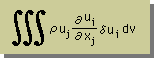
上の式は、少々複雑ですので、理解し易くするために、x-軸方向の成分のみを、下式に引き出してみました。

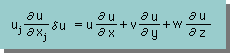
ここで、未知数(u)を、要素の形状関数で近似します。つまり、u=[N]{u}です。すると、上式は、次の様に近似でします。

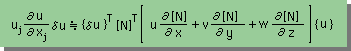
上式の右辺の一部を、下の[C]マトリックスで表すことにします。

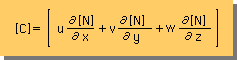
この[C]マトリックスは、８-noded 要素で近似した場合、縦1横8のマトリックスになることに、注意してください。更に、[C]には、u、v、w があります。これらの変数は、未知数として取り扱い線形連立1次方程式で解くことは出来ません。したがって、未知数(u)と[C]マトリックスの(u)とを一致させるためには、繰り返し計算が必要になってきます。

そこで、[C]マトリックスのu、v、w を繰り返し回数の1つ前の、u=[N]{u}^(k-1)、v=[N]{v}^(k-1)、w=[N]{w}^(k-1)をつかって、積分を行います。