■圧縮性流体から非圧縮性流体へ■
最後に、Navier-Stokes equations の疑問を、圧縮性流体から追求してみましょう。前に、連続の式を紹介したときに、流体の弾性係数を考慮した式を導きました。下式がそうです。

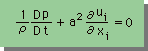
上式を次第に圧縮性流体の型から非圧縮性流体の型にすることを、考えてみましょう。問題を簡単にするために、上式を定常(steady)にします。下式を見て下さい。

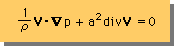
問題は、上式の何を変えれば、圧縮性から非圧縮性流体になるかです。圧縮されにくくなると言うことは、弾性係数が大きくなると言うことです。弾性係数が大きくなると言うことは、圧力の伝播速度(a)が速くなると言うことです。

では、弾性係数が大きくなると、上式の(1/ρ)V・gradp は、どの様に変化するのでしょう。例えば、流体は重力加速度によって動くことを考えると、(1/ρ)V・gradp は、弾性係数が変化しても、ほぼ同じ値を示します。例えば、下図に示すパイプ内の流れを考えて下さい。

流体が水の場合と水銀の場合の(1/ρ)V・∇p は、ほぼ同じですね。最大流速は、ghに比例しますから、流速は流体の種類に関係ありません。また、p=ρgh とおくと、(1/ρ)V・∇p=gV・∇h になり、∇p も流体の種類に関係ないことになります。

このことから、伝播速度(a)が変化しても、a²divV は、ほぼ一定になります。結果的に、伝播速度(a)が大きくなると(つまり弾性係数が大きく)、divVは小さく(→0)なります。

■まとめ■
結果的に、流体の弾性係数が大きくなると、流体は非圧縮性に近ずくことになりますね。言い替えると、非圧縮性流体において、音速は、a=∞になっていることになります。この状態でも、a²divV は、ゼロでないことに注意して下さい。

上の議論をもうちょっと整理すると、圧力勾配が存在する場所では、ゼロ以外のいかなる伝播速度(a)であっても、a²divV は有限な値を示すことになります。上図のパイプ内では、a²divV＞0 になっていることが、上式から確認できます。実際のパイプ内の流れでも、a²divV＞0 になってそうな気がします。

よって、このことからも、divV=0 は、非圧縮性流体を示す方法として、不適切な表現であるこが言えます。したがって、下図が、非圧縮性流体を表すのに、最も適切な方法と言えそうです。